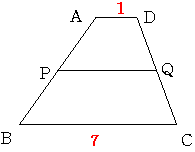
図のようにAD=1 BC=7の台形ABCDがあります。
辺AB上に点Pを 辺DC上に点Qを 線分BCと線分PQが平行となるようにとります。
線分PQによってこの台形の面積が二等分されるときPQの長さはいくらになるでしょうか。
第73回 算数問題 (3月5日〜4月4日)

図のようにAD=1 BC=7の台形ABCDがあります。
辺AB上に点Pを 辺DC上に点Qを 線分BCと線分PQが平行となるようにとります。
線分PQによってこの台形の面積が二等分されるときPQの長さはいくらになるでしょうか。
解答
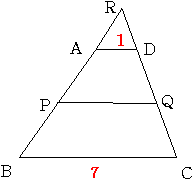
直線BAと直線CDの交点をRとします。
三角形RAD∽三角形RPQ∽三角形RABですから
三角形RADの面積を1とすると三角形RBCの面積は49
条件から
(三角形RAD+三角形RBC)÷2=三角形RPQ であるkとがわかりますから
三角形RPQの面積は(1+49)÷2=25 になります。
よってPQ=5ということがわかります。