∠Aを直角とする直角三角形ABCがあり、AB=12cm AC=6cmとなっています。
辺ABの3等分点をAに近いほうからD,E 辺ACの3等分点をAに近いほうからF,G 辺BCの中点をMとします。
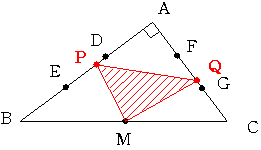
線分DE上に点Pを 線分FG上に点Qをとるとき 三角形PQMの面積の最大値はいくらになるでしょうか。
第72回 算数問題 (2月5日〜3月4日)
∠Aを直角とする直角三角形ABCがあり、AB=12cm AC=6cmとなっています。
辺ABの3等分点をAに近いほうからD,E 辺ACの3等分点をAに近いほうからF,G 辺BCの中点をMとします。

線分DE上に点Pを 線分FG上に点Qをとるとき 三角形PQMの面積の最大値はいくらになるでしょうか。
解答
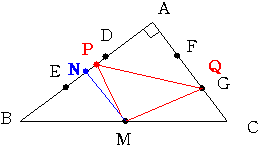
辺ABの中点をNとします。NMとACが平行であることに気をつけてください。
(その1)点Pが線分DN上にあるとき
Pを固定して考えると QがGに一致している時が面積最大であることがわかります。
このような三角形のなかで面積が最大になるようなPの位置を考えると PがDに一致している時となります。
このとき 三角形APQ=三角形ABC×1/3×2/3=三角形ABC×2/9
三角形PBM=三角形ABC×2/3×1/2=三角形ABC×1/3
三角形CQM=三角形ABC×1/3×1/2=三角形ABC×1/6
よって 三角形PQM=三角形ABC×(1-2/9-1/3-1/6)=三角形ABC×5/18
=1/2×12×6×5/18=10
(その2)点Pが線分EN上にあるとき
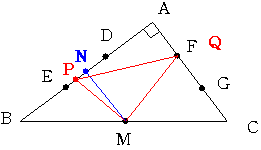
Pを固定して考えると QがFに一致している時が面積最大であることがわかります。
このような三角形のなかで面積が最大になるようなPの位置を考えると PがEに一致している時となります。
このとき 三角形APQ=三角形ABC×1/3×2/3=三角形ABC×2/9
三角形PBM=三角形ABC×1/3×1/2=三角形ABC×1/6
三角形CQM=三角形ABC×2/3×1/2=三角形ABC×1/3
よって 三角形PQM=三角形ABC×(1-2/9-1/6-1/3)=三角形ABC×5/18
=1/2×12×6×5/18=10
その1 その2 より答えは10cm^2となります。