第70回　算数問題　（12月5日〜1月4日）
四辺形ABCDがあります。この四辺形から作られる三角形ABCの重心をP,三角形BCDの重心をQ
三角形CDAの重心をR、三角形DABの重心をSとします。
PR=3cm　QS=5cmであり　PRとQSが直交するとき　この四辺形の面積はいくらになるでしょうか。

解答
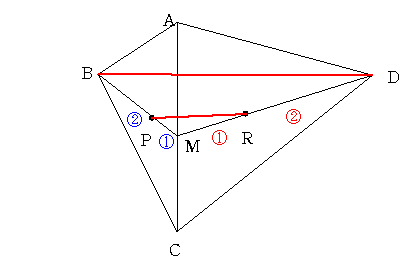
ACの中点をMとします。重心の性質から　BP:PM=2:1　DR:RM=2:1ですから
三角形PMRと三角形BMDは相似で　相似比が１：３
よってBDはPRに平行であり　BD=３×PR=9cmとなります。

同様にACはSQに平行でAC=3×SQ=15cmとなります。
PRとSQが直交するので　BDとACも直交し　四辺形の面積は
1/2×9×15=135/2となります。