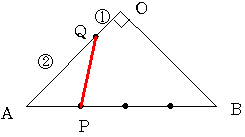
図のように 直角二等辺三角形OABの斜辺AB上にAP:PB=1:3となる点Pを、
辺OA上にOQ:QA=1:2となる点Qをとります。
PQ=17/3cmのとき 直角三角形OABの面積を求めて下さい。
解答
この直角三角形を図のように正方形ABCDの中に埋め込みます。
OQ=①とすると条件からQA=② OC=OA=③となります。
Cを通りQPに平行な直線を引き ABとの交点をRとします。
三角形APQと三角形三角形ARCは相似で相似比はAQ:AC=1:3ですから AP:AR=1:3となり
Rは辺ABの4等分の一つであり CR=17cmであることがわかります。

そこでこの正方形ABCDをさらに下図のような方眼紙に埋め込みます。
方眼紙の1目盛りを④とすると CR=⑰であることがわかりますから
この方眼紙の1目盛りは4cmであることがわかります。
この正方形ABCDの面積は 正方形TUVWから 直角三角形TADを4つ分 除くと求まります。
よって ABCD=20×20-1/2×4×16×4=272
求める直角二等辺三角形の面積は 272×1/4=68cm^2 となります。
