第６7回　算数問題　（9月6日〜10月4日）

１、２、３の数字が書いてあるカードがたくさんあります。このカードを１枚づつ並べたところ
２枚目に並べたカードの数字は、１枚目のカードより数字が小さくはありませんでした。
３枚目に並べたカードの数字は、２枚目のカードより数字が小さくはありませんでした。
このように前に並べたカードの数字より　次に並べたカードの数字のほうが小さくはないことが
９枚目まで続き　１０枚目のカードの数字が初めて９枚目の数字より小さくなりました。

このようなカードの並べ方は何通りあるでしょうか。


解答

最初に　６枚のカードで前のカードの数字よりも次のカードの数字のほうが小さくない場合の数を
出す方法を紹介します。
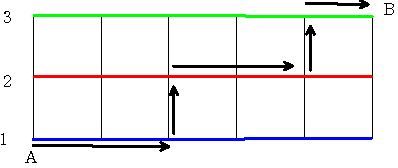
上の図のように格子状の道路でAからBへ行く道順を考えます。図の黒い矢印がその中の
１通りです。
この道の１ブロック分を　青い道を通ったら　１　赤い道を通ったら　２　緑の道を通ったら３　とすると
矢印は１１２２３　となります。
つまり　６枚のカードで前のカードの数字よりも次のカードの数字のほうが小さくない場合の数は図の
AからBへ行くのが何通りあるかを考えるとよいことになります。

（もちろんHやCを使っても出来ます）　

この問題では　９枚目までは前のカードの数字よりも次のカードの数字のほうが小さくないのですから
最初に９枚目までについて考えます

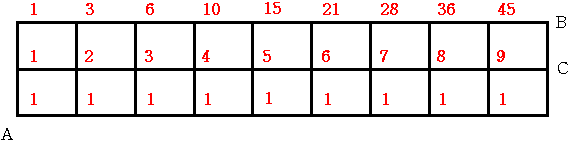
９枚目が３の場合はAからBへ行く経路が４５通りで　このあと１０枚目は１か２ですから
45×２＝９０通り
９枚目が２の場合はAからCへ行く経路が9通りで　このあと１０枚目は１ですから
９通り

合計９９通りとなります。