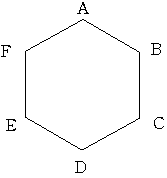
正六角形ABCDEFの頂点Aから出発して、
コインを投げて 表なら時計周りに2つ隣りの頂点に進み
裏なら反時計周りに1つ隣りの頂点に進むものとします。
コインを12回投げて移動を繰り返した時、1度も点Eに止まってらないような移動の仕方は
何通りあるでしょうか
第66回 算数問題 (8月6日〜9月4日)

正六角形ABCDEFの頂点Aから出発して、
コインを投げて 表なら時計周りに2つ隣りの頂点に進み
裏なら反時計周りに1つ隣りの頂点に進むものとします。
コインを12回投げて移動を繰り返した時、1度も点Eに止まってらないような移動の仕方は
何通りあるでしょうか
解答
Aを出発して3回コインを投げた時にどの位置に移動するか考えて見ます。
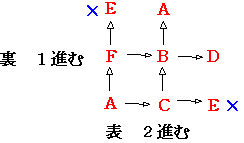
Eに移動してはいけないことを考えると AまたはDに移動することがわかります。
移動の仕方は全部で4通りです。
ではDを出発して3回コインを投げた時にはどの位置に移動するでしょうか
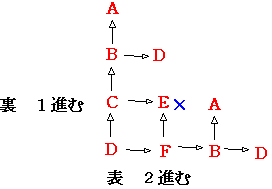
Eに移動してはいけないことを考えると AまたはDに移動することがわかります。
移動の仕方は全部で4通りです。
このことから 3回を1つのサイクルで考えると4サイクルの場合の数を考えることになり
A→(AまたはD)→(AまたはD)→(AまたはD)→(AまたはD)と移動する場合の数は
全部で4×4×4×4=256通り
となります