
忋偺恾偺傛偆偵惓曽宍偑俋偮暲傫偱偄傞恾宍偑偁傝傑偡丅椬傝崌偭偨惓曽宍偵偼摨偠怓傪揾傜側偄傛偆偵
愒丒惵丒墿偺偆偪俀怓埲忋傪巊偭偰揾傝暘偗傞曽朄偼壗捠傝偁傞偱偟傚偆偐丅
偨偩偟夞揮傗忋壓嵍塃偺擖傟懼偊偱堏傝偁偆揾傝偐偨傕偡傋偰嬫暿偡傞暔偲偟傑偡丅
戞俇俆夞丂嶼悢栤戣丂乮7寧5擔乣8寧4擔乯
忋偺恾偺傛偆偵惓曽宍偑俋偮暲傫偱偄傞恾宍偑偁傝傑偡丅椬傝崌偭偨惓曽宍偵偼摨偠怓傪揾傜側偄傛偆偵
愒丒惵丒墿偺偆偪俀怓埲忋傪巊偭偰揾傝暘偗傞曽朄偼壗捠傝偁傞偱偟傚偆偐丅
偨偩偟夞揮傗忋壓嵍塃偺擖傟懼偊偱堏傝偁偆揾傝偐偨傕偡傋偰嬫暿偡傞暔偲偟傑偡丅

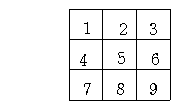
曋媂忋丂惓曽宍偵斣崋傪偮偗傑偡丅怓傪A,B,C偲偟傑偡丅
惓曽宍俆偵怓A傪揾偭偨偲偟偰峫偊傑偡
嘥丂惓曽宍俆偺廃傝偑係偮偲傕怓B偺応崌
惓曽宍侾丆俁丆俆丆俈丆俋偼怓A,C偺俀捠傝偱偁傞偐傜
俀偺係忔=侾俇捠傝
嘦丂惓曽宍俆偺廃傝偺偆偪俁偮偑怓B偺応崌
惓曽宍俀丆係丆俇偑怓B偱偁傞偲偒丂惓曽宍俉偼怓C
惓曽宍侾丆俁偼怓A,C偺俀捠傝
惓曽宍俈丆俋偼怓A
傑偨丂俆偺廃傝偺俁偮偺庢傝曽偼係捠傝
傛偭偰係亊俀亊俀=侾俇捠傝
嘨丂惓曽宍俆偺廃傝偺偆偪俀偮偑怓B偺応崌
丂丂
丂丂嘨-嘥岦偐偄偑摨怓偺偲偒
丂丂丂丂惓曽宍俀丆俉傪怓B丂惓曽宍係丆俇傪怓C偲偡傞
丂丂丂丂惓曽宍侾丆俁丆俆丆俈丆俋偼怓A
丂丂丂丂傛偭偰侾捠傝
丂丂嘨-嘥岦偐偄偑摨怓偱側偄偲偒
丂丂丂丂惓曽宍俀丆俇傪怓B丂惓曽宍係丆俉傪怓C偲偡傞
丂丂丂丂惓曽宍俁偼怓A,C丂惓曽宍俈偼怓A,B丂惓曽宍侾丆俋偼怓A
丂丂丂丂傑偨岦偐偄偑摨怓偱側偄揾傝曽偼俀捠傝
丂丂丂丂傛偭偰丂俀亊俀亊俀亖俉捠傝
怓A,B,C偺寛傔曽偼俁亊俀亊侾捠傝偱偁傞偐傜
俇乮16+16+1+8)=246捠傝