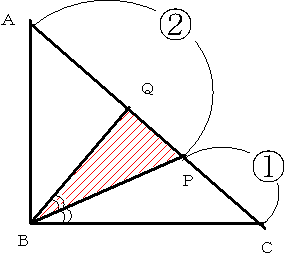
一辺の長さが42cmの直角二等辺三角形ABCの斜辺ACを2:1の比に内分する点をPとします。
線分AP上に 角CBP=角PBQとなる点Qをとります。
このとき 三角形BPQの面積はいくらになるでしょうか。
第64回 算数問題 (6月5日〜7月4日)

一辺の長さが42cmの直角二等辺三角形ABCの斜辺ACを2:1の比に内分する点をPとします。
線分AP上に 角CBP=角PBQとなる点Qをとります。
このとき 三角形BPQの面積はいくらになるでしょうか。
解答

図のように 一辺が14cmの格子状の補助線を引き、BとSを結ぶと、
三角形BDRと三角形BRSは直角をはさむ二辺の比が2:1で相似であることがわかります。
よって ACとBSの交点はQに他なりません。
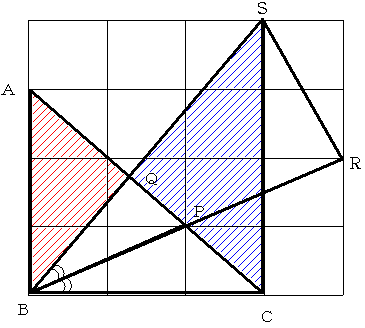
次に三角形ABQと三角形CSQは相似ですから
AQ:QC=3:4
よって AQ:QP:PC=3/7:(1-3/7-1/3):1/3=9:5:7
これより三角形BPQの面積は 三角形ABCの面積の5/21となり
1/2×42×42×5/21=210cm^2 となります。