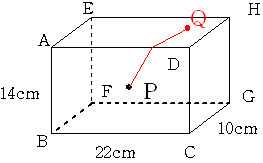
直方体ABCD-EFGHがあり AB=14cm BC=22cm CG=10cmであるとします。
この一つの面ABCDの真ん中に点Pをとります。
点Qをこの直方体上にとり 点Pと点Qを できるだけPQの長さが短くなるように 糸で結びます。
このとき PQが一番長くなるときの長さはいくらになるでしょうか。
第62回 算数問題 (4月5日〜5月4日)

直方体ABCD-EFGHがあり AB=14cm BC=22cm CG=10cmであるとします。
この一つの面ABCDの真ん中に点Pをとります。
点Qをこの直方体上にとり 点Pと点Qを できるだけPQの長さが短くなるように 糸で結びます。
このとき PQが一番長くなるときの長さはいくらになるでしょうか。
解答
Pの真裏の点Rまでの距離は22+10=32 または 14+10=24 であるから
PR=24が最長であるように思いますが じつは もっと長い点があります。
展開図を考えてみましょう。

上の図は展開図で 同じ文字は同じ頂点であると考えます(たとえば AとA'とA''は同じ頂点)
ここで 青い線がPからの長さが24cmのところですからこの円の外の点は 24cmより長い
たとえばP'R=32cmですから P'R上の点で Rのちょっと右の点はPからの最短距離が24cmより
長くなります。
求める点は P'R上にあることは 容易にわかりますから
PQ=P'Qとなる点が求める点となります。
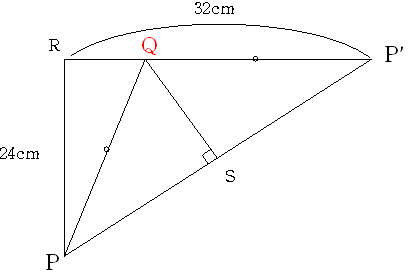
すると 直角三角形PP'Rは3:4:5の直角三角形ですから PP'=40
PS=20
直角三角形P'QSも3:4:5の直角三角形ですから P'Q=25 となります。