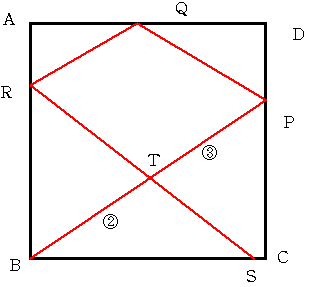
曈AB丂CD丂DA偑嬀偵側偭偰偄傞惓曽宍ABCD偑偁傝傑偡丅
揰B偐傜敪幩偟偨岝偑恾偺傛偆偵斀幩偟偰曈BC忋偺揰S偵払偟傑偟偨丅
偙偺偲偒丂岝偑岎嵎偟偨揰傪T偲偡傞偲丂BT:TP=2:3偱偁偭偨偦偆偱偡丅
偙偺偲偒惓曽宍ABCD偲巐妏宍PQRT偺柺愊斾偼偄偔傜偵側偭偰偄傑偡偐丅
丂丂丂
怣嶰偝傫偺夝摎
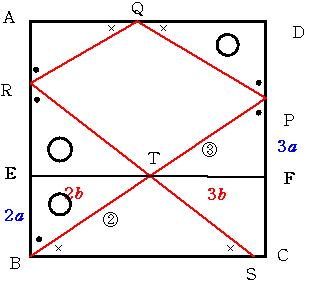
俿傪捠偭偰俙俢偵暯峴慄傪堷偒曈俙俛丄俠俢偲偺岎揰傪偦傟偧傟俤丄俥偲偡傟偽丄
嶰妏宍俿俤俛丆俿俥俹偼憡帡偱憡帡偺斾偼俀丗俁丅
慄暘俤俛偺挿偝傪俀倎丄俿俤偺挿偝傪俀倐偲偡傞偲丄俥俹亖俁倎丄俿俥亖俁倐丅
嶰妏宍俿俤俛丄俿俤俼丄俻俢俹偼崌摨丅嶰妏宍俿俥俹丄俻俙俼偼崌摨丅
惓曽宍偺堦曈偺挿偝偼丄倎傪扨埵偵偡傞偲俈倎丄倐傪扨埵偵偡傞偲俆b丅
惓曽宍偐傜慄暘俤俥傛傝壓偺挿曽宍偲係屄偺嶰妏宍偺柺愊傪堷偔偲
乮倎x們傪扨埵偲偟偰乯俁俆亅侾侽亅俋亅係亖侾俀丅廬偭偰丄摎偊偼丂俁俆丗侾俀丅
傎偘丂偺夝摎

摨偠妏搙偵偟傞偟傪偮偗傑偟偨丅
BT=嘇偲偡傞偲丂嶰妏宍BTS偼擇摍曈嶰妏宍偱偡偐傜丂TA=嘇
嶰妏宍BTR偼擇摍曈嶰妏宍偱偡偐傜丂RT=嘇
傛偭偰丂RS=嘋
傑偨丂巐妏宍PQRT偼暯峴巐曈宍偱偡偐傜丂PQ=嘇丂QR=嘊偱偁傞偙偲偑傢偐傝傑偡丅
