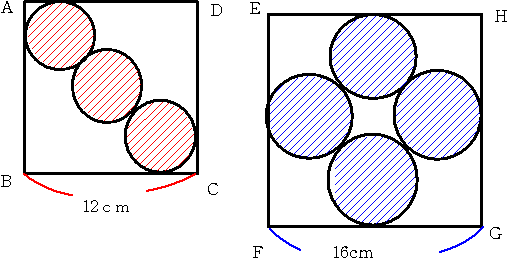
下の図のように 一辺の長さが12cmの正方形ABCD および 一辺の長さが16cmの正方形EFGHの
内部に接するように 同じ大きさの円が互いに接して描かれています。
このとき 青い円の半径は 赤い円の半径の何倍になっているでしょうか。
解答
第57回 算数問題 (11月5日〜12月4日)
下の図のように 一辺の長さが12cmの正方形ABCD および 一辺の長さが16cmの正方形EFGHの
内部に接するように 同じ大きさの円が互いに接して描かれています。
このとき 青い円の半径は 赤い円の半径の何倍になっているでしょうか。

解答

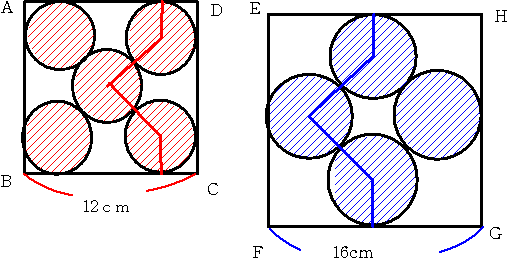
正方形ABCDに さらに2つ円を描き 図のように赤い線と青い線を描きます。
するとこの線は相似であることがわかります。相似比は 12:16=3:4ですから
半径の比も3:4 答えは 4/3倍ということになります。
同じ大きさの正方形であるときは 3つ 4つ 5つ 入った円の半径はずべて同じになるということですね。