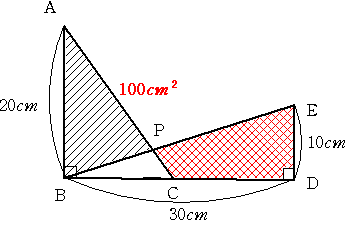
2つの直角三角形ABCとBDEが図のように重なっている。ACとBEの交点をPとする。
AB=20cm DE=10cm BD=30cm 三角形ABPの面積が100cm2であるとき
四角形CDEPの面積を求めてください。
第56回 算数問題 (10月5日〜11月4日)

2つの直角三角形ABCとBDEが図のように重なっている。ACとBEの交点をPとする。
AB=20cm DE=10cm BD=30cm 三角形ABPの面積が100cm2であるとき
四角形CDEPの面積を求めてください。
解 答

ACの延長とEDの延長の交点をQとします
三角形ABEの面積は1/2×20×30=300cm^2ですから
三角形APEの面積は300-100=200cm^2です
三角形ABP と 三角形APEの面積比は 100:200=1:2なので
BP:PE=1:2となります。
三角形ABPと三角形QEPは相似で 相似比がBP:EP=1:2ですから EQ=40cmとなり
これよりQD=30cmとなります。
三角形ABPと三角形QDCは相似で相似比がAB:QD=20:30=2:3ですから
BC:DC=2:3 BC=30×2/5=12cm CD=30×3/5=18cmとなります。
四角形CDEP=三角形CDE+三角形PCE=1/2×18×10+三角形BCE×2/3
=90+1/2×12×10×2/3=90+40=130cm^2
となります。