
戞55夞丂嶼悢栤戣丂乮8寧4擔乣9寧4擔乯
懢榊孨偼A抧揰偐傜B抧揰傊岦偐偭偰丂師榊孨偼丂B抧揰偐傜A抧揰偵岦偐偭偰摨帪偵弌敪偟丄
A抧揰偲B抧揰偺娫傪媥傑偢偵壗搙偐摨偠懍偝偱墲暅偟傑偟偨丅
丂擇恖偼嵟弶偵弌夛偭偨抧揰偐傜4km偼側傟偨抧揰偱俀夞栚偵弌夛偄,俀夞栚偵弌夛偭偨抧揰偐傜
2km偼側傟偨抧揰偱俁夞栚偵丂弌夛偄傑偟偨丅搑拞偱師榊偔傫偼壗夞偐懢榊孨偵捛偄墇偝傟偨偐傕
偟傟傑偣傫丅乮捛偄墇偟偨偺偼弌夛偭偨偙偲偵偼側傝傑偣傫乯
懢榊孨偲師榊孨偺懍偝偺斾傪媮傔偰偔偩偝偄丅
俀偮埲忋偺摎偊偑偁傞偲偒偼斾偺抣偺彫偝偄弴偵僇儞儅偱嬫愗偭偰偔偩偝偄丅
夝摎

暥復偺撪梕偐傜丂懢榊孨偺曽偑憗偄偐摨偠憗偝偱偁傞偲峫偊偰偔偩偝偄丅
乮栤戣偺暥復偩偗偱偼丂師榊孨偺曽偑憗偄偙偲傕峫偊傜傟傑偡偑乯
侾夞栚偵弌夛偭偨偺偑丂AB偺娫偺P抧揰偱偡丅弌敪偐傜丂弌夛偆傑偱偺帪娫傪嘆偲偟傑偡丅
俀夞栚偵夛偆傑偱偵嘇偺帪娫偑宱夁偟傑偡丅師榊孨偼丂A傪捠夁偟偰偄傞応崌偲捠夁偟偰偄側偄応崌偑偁傝傑偡丅
嘥丂師榊孨偑A傪捠夁偟偰偄傞応崌

俀夞栚偵弌夛偭偨応強Q偼AP偺娫偱偡丅Q偑PB偺娫偲偡傞偲丂嘇偺帪娫偱丂師榊孨偑AP偺俀攞埲忋傪堏摦偡傞偙偲偵側傝嵟弶偺忦審偵偁傢側偄偐傜偱偡丅
偡傞偲丂師榊孨偼丂嘇偺帪娫偱丂懢榊孨偺恑傓嫍棧傛傝4km彮側偄偺偱丂懢榊孨偲師榊孨偺嘆帪娫偁偨傝偵恑傓嫍棧偺嵎偼2km偱偁傞偙偲偑傢偐傝傑偡丅
偮傑傝丂
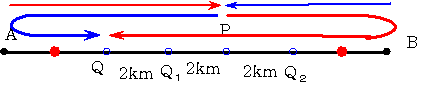
傛偭偰AQ=BQ2丂QQ侾=Q侾P=PQ俀=2km丂偲偟偰丂忋偺恾偺傛偆偵恑傫偱偄傞偲峫偊傜傟傑偡丅
偙偺偁偲懢榊孨偼丂AQ偺俀攞+8km恑傓偙偲偵側傞偺偱偡偑丂偦偺揰偼QQ俀=0丂偲偟偰傕丂偣偄偤偄揰P偱偁傝丂揰Q侾傛傝偼
塃懁偵側傝傑偡偐傜丂俁夞栚偵弌夛偆抧揰偼丂忦審傪枮偨偝側偄偙偲偑傢偐傝傑偡丅
嘦丂師榊孨偑A傪捠夁偟偰偄偄側偄応崌

丂偙偺偲偒偼丂嘇扨埵帪娫偁偨傝師榊孨偑恑傓嫍棧偼4km偱偁傞偙偲偑傢偐傝傑偡丅
偙偺偁偲丂偝傜偵嘇扨埵帪娫偨偭偨屻偵擇恖偑弌夛偆応強傪R偲偡傞偲丄R偼
A偱愜傝曉偟偰AQ偺娫偺応崌偲丂PQ偺娫偺応崌偑偁傝傑偡丅
嘦-1丂R偑AQ偺娫偺偲偒

忋偺傛偆偵丂AR娫偺嫍棧偑1km偱偁傞偙偲偵側傝傑偡偐傜
嘆扨埵帪娫摉偨傝偵恑傓嫍棧偼丂懢榊孨7km丂師榊孨2km丂懍偝偺斾偼7:2偲側傝傑偡丅
嘦-1丂R偑PQ偺娫偺偲偒
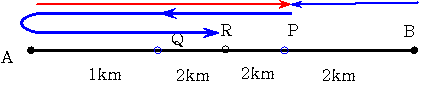
忋偺傛偆偵丂AQ娫偺嫍棧偑1km偱偁傞偙偲偵側傝傑偡偐傜
嘆扨埵帪娫摉偨傝偵恑傓嫍棧偼丂懢榊孨5km丂師榊孨2km丂懍偝偺斾偼5:2偲側傝傑偡丅