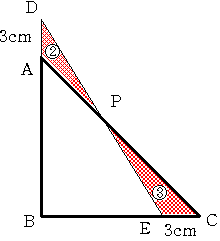
下の図のように直角二等辺三角形ABCの辺ABをAのほうに延長しその延長線上に点Dを、また 辺BC上に点Eを
AD=BC=3cmとなるようにとります。ACとDEの交点をPとします。
三角形ADPと三角形CEPの面積比が2:3となりました。
このとき四角形ABEPの面積を求めてください。。
第53回 算数問題 (6月5日~7月4日)
下の図のように直角二等辺三角形ABCの辺ABをAのほうに延長しその延長線上に点Dを、また 辺BC上に点Eを
AD=BC=3cmとなるようにとります。ACとDEの交点をPとします。
三角形ADPと三角形CEPの面積比が2:3となりました。
このとき四角形ABEPの面積を求めてください。。

解答
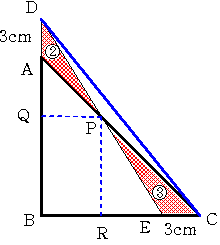
上の図のようにDCを結び またPからAB BCへ垂線を下ろし その足をQ,Rとします。
最初に 三角形ADCと 三角形CEDの面積を比較します。
ともに3cmの辺 AD CEを底辺と考えると
三角形ADCの高さは 二等辺三角形ABCと同じ高さ
三角形CEDの高さは 二等辺三角形ABCの高さより3cmだけ高い
よって三角形CEDの面積は 三角形ADCの面積より 1/2×3×3=9/2cm^2だけ多いことがわかります。
この三角形CED 三角形ADCから共通の三角形CDPを除いた三角形ADPと三角形CEPの面積の差も9/2で
この差が ③-②=①ですから ②=9/2×2=9cm^2であることがわかります。
三角形ADPの面積から PQは9÷3×2=6cm
PRは 6×3/2=9cmとなり 三角形APQ は二等辺三角形ですから
AQ=6cm であり AB=15cmであることがわかります。
よって四角形ABEP=三角形APC-三角形PEC=1/2×(15×15-3×9)=99cm^2 となります。