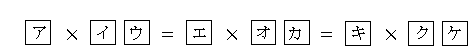戞51夞丂嶼悢栤戣丂乮4寧5擔乣5寧4擔乯
壓偵偁傞幃偼侾働僞偺悢偲俀働僞偺悢偺妡偗嶼偺摎偊偑摍偟偄偙偲傪偁傜傢偟偰偄傞偲偟傑偡丅
傾偐傜働偵偼丂侾偐傜俋傑偱偺悢偑侾夞偯偮擖傞偲偟傑偡丂傾傛傝僄偑戝偒偔丂僄傛傝僉偑戝偒偄偲偒
傾僀僂僄僆僇僉僋働傪暲傋偨悢偼偄偔傜偱偟傚偆偐丅
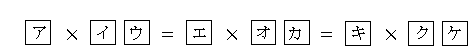
傾僄僉偺戝彫傪峫偊偢偵摎偊傪傕偲傔傛偆丅
嬼悢偼2,4,6,8偺係偮偁傞偐傜丂丂傾僄僉僂僇働偺偳偙偐偵擖傞丅傛偭偰偙偺愊偼嬼悢偲側傞丅
傑偨丂偙偺愊偑俆偺攞悢偱偁傞偲偡傞偲丂5偑壗夞傕巊傢傟傞偙偲偵側傞偐傜丂5偼丂僀僆僋偺偳偙偐偵擖傞丅
偙偺愊偼俆偺攞悢偱偼側偄
傛偭偰僀偵俆偑擖傞偲偟偰丂僀僂偺悢帤偼丂51偐傜59偺偄偢傟偐偵側傞偲偟偰傛偄
嘆僀僂偑51偺偲偒丂
51=3亊17偱偁傞偐傜丂僆僇丂僋働偼侾俈偺攞悢偱偁傞丅
俀寘偺17偺攞悢偼丂17丂34丂51丂68丂85丂丂
51偑巊傢傟傞偺偱侾俈,丂85偼巊傢傟側偄乮侾丂5丂偑廳暋乯丂傛偭偰丂俀寘偺俁偮偺悢偼丂34丂51丂68
偙偺偲偒丂傾僀僂偵7偲偄偆悢帤偼侾夞偟偐巊傢傟側偄偐傜俁偮偺悢偑偡傋偰俈偺攞悢偵側傞偙偲偼側偄
摎偊偼側偄
嘇僀僂偑52偺偲偒丂
52=4亊13偐傜丂僆僇丂僋働偼侾3偺攞悢偱偁傞丅
俀寘偺13偺攞悢偼丂13丂26丂39丂52丂65丂78丂91丂丂
52偑巊傢傟傞偺偱26,丂65偼巊傢傟側偄乮侾丂5丂偑廳暋乯丂傛偭偰丂2寘偺悢偼丂13丂39丂78丂91
91偑巊傢傟傞偲偡傞偲丂52丂78丂91丂偲側傝丂91偩偗偑7偺攞悢偱丂愊偼7偺攞悢偲側傞偑丂傾僄僉偵俈偼偼偄傜側偄丂
91偑巊傢傟側偄偲偡傞偲
丂丂丂丂丂丂13丂52丂78丂偺偲偒偼丂52=13亊4丂偲丂78=13亊6偺嵟彫岞攞悢偼丂13亊12偱偁傞偐傜丂13亊1寘偵偼側傜側偄
丂丂丂丂丂丂39丂52丂78丂偺偲偒偼丂52=13亊4丂偲丂78=13亊6偺嵟彫岞攞悢偼丂13亊12偱偁傞偐傜丂傾僀僂偺側偐偵1偼擖傜側偄
摎偊偼側偄
嘊僀僂偑53偺偲偒
53偼慺悢偱偁傞偐傜丂53偺攞悢偺俀寘偺悢偼俁偮側偄
摎偊偼側偄
嘋僀僂偑54偺偲偒
5-1丂悢帤偺侾偑侾寘偺悢偲偟偰巊傢傟傞帪
丂丂丂丂傾亊54丂1亊僄僆偺傛偆偵巊傢傟傞帪丂傾偵偼俀埲忋偺悢偑偼偄傞偺偱丂偙偺愊偼2寘偵側傞
丂丂丂丂傛偭偰僄僆偵擖傞悢偼側偄偙偲偑傢偐傞
丂丂丂丂1亊54=僂亊僄僆=僇亊僉僋丂偲側傞偲偒丂僄僆丂僉僋偵偼丂54偺栺悢偑擖傞偺偱丂27丂18
丂丂丂丂偙偺偲偒1偑廳暋偟偰偄傞偺偱摎偊偼側偄
5-俀丂丂悢帤偺侾偑俀寘偺侾偺埵偺悢偲偟偰巊傢傟傞帪
丂丂丂傾亊27亊2=僂亊僄1偲側傞偺偱丂僄侾偼俋偺攞悢偵側傞
丂丂丂丂丂乮俋偺攞悢偱側偄帪偼丂僂偑俋偺攞悢偐偮俀偺攞悢偵側傝摉偰偼傑傞悢帤偼側偄乯
丂丂丂僄=8丂偱偁傞偐傜丂傾偼俁偺攞悢偱丂傾亖3,6,9丂偙偺偲偒丂僂亖2,4,6丂4偼巊偊側偄偐傜俀捠傝
丂丂丂丂丂3亊54=2亊81偺偲偒丂巆傝偺悢偼丂6,7,9偱嵟掅偱傕6亊7仜傑偨偼7亊6仜丂偱420傪挻偊傞悢偵側傞偐傜
丂丂丂丂摎偊偼側偄
俆亅俁丂悢帤偺侾偑俀寘偺悢偺侾侽偺埵偺悢偲偟偰巊傢傟傞偲偒
丂丂丂丂丂傾亊27亊2=僂亊1僆偲側偭偰偄傞
丂丂丂5-3-1丂侾僆偑9偺攞悢偺偲偒丂1僆=18丂偱傾亊54=僂亊18丂傾丗僂=1:3
丂丂丂丂丂丂丂丂巊傢傟偰側偄悢帤偱偙傟傪傒偨偡偺偼丂傾=2丂僂亖俇丂傑偨偼丂傾亖3丂僂亖俋
丂丂丂丂丂丂丂俀亊俆係=俇亊侾俉偺偲偒丂巆傝偺悢偼丂3,7,9偱偙偺悢傪巊偭偰嬼悢偵偼側傜側偄
丂丂丂丂丂丂丂3亊54=9亊18偺偲偒丂巆傝偺悢偼丂2,6,7偱2+6=8丂6+7=13偱偁傞偐傜丂偙偺2,6傑偨偼6,7傪巊偭偨俀寘偺悢偼9偺攞悢偵側傜側偄
丂丂丂丂丂丂傛偭偰丂6亊27偺傒偑忦審傪枮偨偡摎偊偲側傞
丂丂丂5-3-2丂1僆偑9偺攞悢偱側偄偲偒丂僂=9偲側傞偐傜丂1僆偼6偺攞悢偱侾僆=12丂18丂18偼9偺攞悢偩偐傜偙偙偱偼奩摉偟側偄
丂丂丂丂丂丂丂2亊5係=9亊12偺偲偒丂2偑廳暋丂
嘍僀僂偑56偺偲偒
5-1丂悢帤偺侾偑侾寘偺悢偲偟偰巊傢傟傞帪
丂丂丂丂傾亊56丂1亊僄僆偺傛偆偵巊傢傟傞帪丂傾偵偼俀埲忋偺悢偑偼偄傞偺偱丂偙偺愊偼2寘偵側傞
丂丂丂丂傛偭偰僄僆偵擖傞悢偼側偄偙偲偑傢偐傞
丂丂丂丂1亊56=僂亊僄僆=僇亊僉僋丂偲側傞偲偒丂僄僆僉僋丂偼56偺栺悢偲側傞偺偱丂28丂14
丂丂丂丂偟偐偟1偑廳暋偟偰偄傞偺偱偙偺傛偆偵偼側傜側偄偙偲偑傢偐傞
5-俀丂丂悢帤偺侾偑俀寘偺侾偺埵偺悢偲偟偰巊傢傟傞帪
丂丂丂傾亊7亊8=僂亊僄1偲側傞偺偱丂僂偼8偱偁傝丂傾亊7=僄侾偲側偭偰偄傞偺偱丂傾亖3丂僄亖2偲側傝
丂丂丂丂俁亊俆俇=俉亊俀侾丂偺偙傝偺悢係,俈,俋偱俉偺攞悢偼偱偒側偄丂
丂丂丂丂(係亊仜仜偼係偺攞悢丂丂仜亊仜係偼俀偺攞悢偲側傞偐傜乯
俆亅俁丂悢帤偺侾偑俀寘偺悢偺侾侽偺埵偺悢偲偟偰巊傢傟傞偲偒
丂丂丂丂丂傾亊7亊8=僂亊1僆偲側偭偰偄傞
丂丂丂5-3-1丂侾僆偑7偺攞悢偺偲偒丂1僆=14丂偱僂偼係偺攞悢偲側傞偑丂4偼偮偐傢傟偰偄傞偺偱丂僂=8
丂丂丂丂丂丂丂丂傾=2偲側傝丂丂2亊56=8亊14丂偺偙傝偺悢丂3,7,9偱8偺攞悢偼嶌傟側偄
丂丂丂5-3-2丂1僆偑7偺攞悢偱側偄偲偒丂僂=7偲側傞偐傜丂1僆偼8偺攞悢偱侾僆=侾俇丂偟偐偟俇偼巊傢傟偰偄傞
傛偭偰摎偊偼側偄
嘐僀僂偑57偺偲偒
57=3亊19偱偁傞偐傜丂僆僇丂僋働偼侾9偺攞悢偱偁傞丅
俀寘偺19偺攞悢偼丂19丂38丂57丂76丂95丂
57偑巊傢傟傞偺偱76丂95偼巊傢傟側偄乮5丂7丂偑廳暋乯丂傛偭偰丂2寘偺悢偼丂19丂38丂57
57偼3偺攞悢偱偁傞偐傜丂19丂38偵妡偗傜傟傞1寘偺悢偼3偺攞悢偱偁傞偑丂巆偭偰偄傞3偺攞悢偼6偟偐側偄偐傜
忦審傪枮偨偡摎偊偼側偄
嘑僀僂偑58偺偲偒
丂丂58=2亊29偱偁傞偐傜丂僆僇丂僋働偼29偺攞悢偱偁傞丅
俀寘偺29偺攞悢偼丂29丂58丂87
58丂87偼摨帪偵巊傢傟側偄乮8丂偑廳暋乯丂傛偭偰丂忦審傪枮偨偡2寘偺悢偼側偄
嘒僀僂偑59偺偲偒
59偼慺悢偱偁傞偐傜59偺攞悢偺俀寘偺悢偼俁偮側偄
摎偊偼側偄
埲忋偐傜丂3亊54=6亊27=9亊18丂偑摎偊偲側傞
354627918