第49回　算数問題　（2月5日〜3月4日）

P町　と　Q町　を　往復する　二つのバスが走っています。
バスAは　この区間を21分で走行し、到着後に2分の休憩をしてから　また出発します。
バスBは　この区間を31分で走行し、到着後に1分の休憩をしてから　また出発します。
あるとき両方のバスが同時にP町を出発してP町とQ町の間を何回か行き来　したあと
2時間39分後に同時にQ町へ到着しました。
この間に２つのバスは何回かすれ違いますが　すれ違ったときに　
「同時にP町を出発してからのすれ違うまでの時間」　を書き留めるものとします。
2時間39分後にその数値を合計すると何分になるでしょうか。

答えは分に直してください。また　最後の　2時間39分=159分は答えに入らないものとします。

たとえば　３回すれ違った時は　　1分+20分+300分=321分　321が答えになります
P町およびQ町でバスが同時に休憩することはありません。（調べればわかるけど…）


解答　397.5分
最後の１行がヒントであると気がついたでしょうか

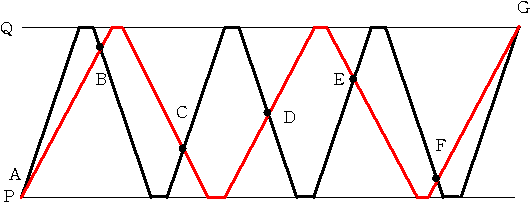
ダイヤグラムを書いて見ます。

AからBまでの時間をABとかくことにします。
この図形はDに関して点対称ですね　ということは　AB=FG　AC=EG　AD=DGとなるので
AB+AC+AD+AE+AF=(AB+AF)+(AC+AE)+AD=159+159+159/2=159×2.5=397.5となるわけです。

解答２
とはいえ心配な方もいらっしゃるでしょうから時間をいれたダイヤグラムも描いて見ます

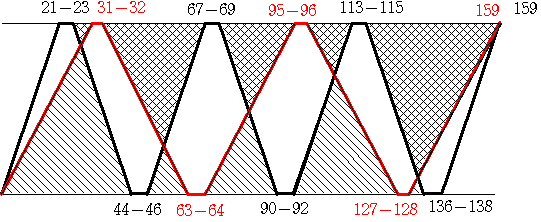
三角形の相似を使って各々の時間を求めます（三角形の名称　省略）
Bの時間　三角形の相似比が(31-23):44=2:11なので
　　　　　　　23と44を2：11に内分　(23×11+44×2)/13=341/13
Cの時間　三角形の相似比が(67-32):(63-46)=35:17なので
　　　　　　　32と63を35：17に内分　(32×17+63×35)/52=2749/52
Ｄの時間　三角形の相似比が(95-69):(90-64)=1:1なので
　　　　　　　69と90を1：1に内分　(69+90)/2=159/2
Eの時間　三角形の相似比が(113-96):（127-92=17:35なので
　　　　　　　96と127を17：35に内分　(96×35+127×17)/52=5519/52
Fの時間　三角形の相似比が(159-115):(136-128)=11:2なので
　　　　　　　115と136を11：2に内分　(115×2+136×11)/13=1726/13

合計　341/13+2749/52+159/2+5519/52+1726/13
　　　=(341+1726）/13+(2749+5519）/52+159/2
　　　=159+159+159/2
　　　=159×2.5=397.5