第48回　算数問題　（1月5日〜2月4日）

AB=6cm　BC=8cm　CA=10cm　の　三角形ABC　がある。半径１の円の中心が　この三角形の辺または頂点を中心として

　A→B→C→A　と動く時　この円が通過する部分の面積を求めて下さい



解答



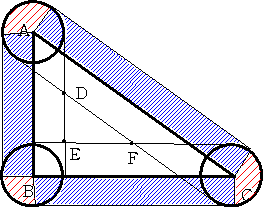
三角形ABCの外側の面積と内側の面積とを分けてもとめます。

外側の面積は図の赤い斜線の部分と青い部分の面積になります。

　赤い部分の面積
を３つ集めてくっつけると円になるので　面積は　１×１×3.14=3.14

　青い部分の面積　6×1+８×１+10×1=24

合計　3.14+24=27.14


三角形ABCの内側の面積は三角形ABCから　三角形DEF（D,E,Fは上の図の点のこと）の面積を引くと出てきます。
そのためにまず三角形DEFの各辺の長さを求めます。
D,E,Fから三角形に垂線を引いて　図のように記号をつけます。

三角形ABCと三角形DEFは相似ですから　DE=3x　EF=4x　FD=5xと置くと
AB+BC-AC=6+8-10
(AG'+3x+1)+（１＋4ｘ＋H'C）-(AG+5x+HC)=4　　　
　AG'=AG　H'C=HCであるから
2x+2=4
x=1

内側の面積は　三角形ABC-三角形DEF=1/2×6×8-1/2×3×4=18

よって　全体の面積は　27.14+18=45.14cm^2となります