第46回　算数問題　（11月5日〜12月4日）

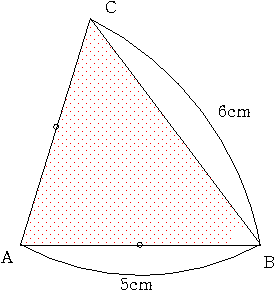
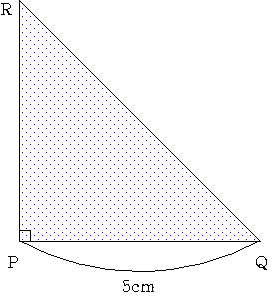
下の図のように　AB=AC=5cm　BC=6cmの二等辺三角形ABCと　PQ=5cmの直角二等辺三角形を
AとP　BとQが一致し、C,Rが辺ABの上部に来るように重ねました。
このとき　四角形ABCRの面積を求めてください

重ねる前

重ねた図

　　解答

図のように　BCの中点をMとしてAMを一辺とする正方形AKLMを描きます。
すると三角形ABMと三角形AKRは合同ですから
四角形ABCRの面積は五角形AMCRKと同じになります。
そして　これは　正方形から　三角形CLRを除いた面積ですから
4×4-1/2×1×1=15.5cm^2となります。