第45回　算数問題　（10月2日〜11月4日）

0から５までの数字を使った８けたの数で（使っていない数字があってもよい）　隣どおしのけたの数の差が１であるような
数はいくつあるでしょうか。
たとえば　12343210　12121212　のような数字を考えてください。

解答(miya さん）
エクセルで処理する

解答（浜田　明巳さん）

上の位からａ(１)〜ａ(８)とする．再帰を使い，シラミつぶしにａ(ｎ)（１≦ｎ≦８）を求める．まず１≦ａ(１)≦５であり，
　　ａ(ｎ)＝ａ(ｎ−１)−１，ａ(ｎ−１)＋１（２≦ｎ≦８）
そしてその個数を求め，それを答とする．
　このマクロにより，答は３０５個となる．

Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Range("A1").Select
Dim a(8) As Integer
Call saiki(1, a())
Range("A1").Select
End Sub
Sub saiki(ByVal n As Integer, ByRef a() As Integer)
Dim max As Integer
Dim steppu As Integer
Dim j As Integer
If n = 1 Then
a(1) = 1
max = 5
steppu = 1
Else
a(n) = a(n - 1) - 1
max = a(n - 1) + 1
steppu = 2
End If
While a(n) <= max
If 0 <= a(n) And a(n) <= 5 Then
If n < 8 Then
Call saiki(n + 1, a())
Else
Cells(1, 1).Value = Cells(1, 1).Value + 1
For j = 1 To 8
Cells(Cells(1, 1).Value, j + 1).Value = a(j)
Next j
Range("B" & Cells(1, 1).Value).Select
End If
End If
a(n) = a(n) + steppu
Wend
End Sub

解答

上のような図を考えます。青い数字の２は最初の数を示します。
上に進んだ時は前の数に１を足し右に進んだ時は前の数から１を引くことにします。
赤い線を進んだ時は　２→１↑２→１→０↑１↑２→１　で　21210121　という条件に合った数ができます。
青い線を進んだ時は　２↑３↑４↑５↑６→５→４→３　で　23456543　という条件には合わない数ができます。

このことからここから赤い斜線の範囲内で７歩進む場合の数を考えるとよいことがわかります。
（下の赤い斜線は0より減らないように　上の赤い斜線は５より増えないように　境界線というわけです）

最初の数字が１のときは…

19+28+14==61通りあります。

最初の数字が2のときは…

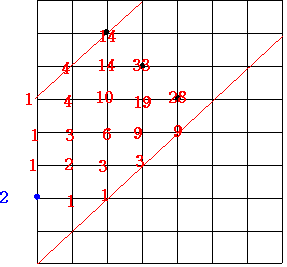
14+33+28=75通りあります

最初の数が３のときは…
　たとえば34543210　という数は　各位の数を５から引くと　21012345　となります。
このようにすると　3で始まる数と２で始まる数は1:1に対応しますから　75通りであることがわかります

最初の数が４のときは…
　たとえば43454321　という数は　各位の数を５から引くと　12101234　となります。
このようにすると　1で始まる数と２で始まる数は1:1に対応しますから　61通りであることがわかります　

最初の数が5のときは…

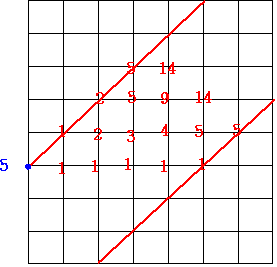
14+14+5=33　通りあります

以上から　2(61+75)+33=305

305　通りあることがわかりました