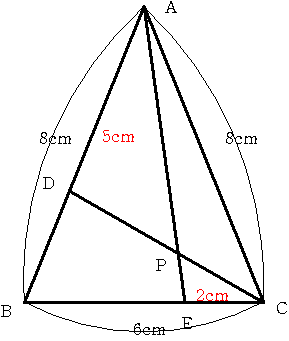
壓偺恾偺傛偆偵AB=AC=8cm丂BC=6cm偺擇摍曈嶰妏宍偑偁傝傑偡丅
曈AB忋偵丂AD=5cm丂曈BC忋偵CE=2cm偲側傞揰D,E傪偲傝傑偡丅
AE偲CD偺岎揰傪P偲偡傞偲偒丂AP:CP傪娙扨側惍悢斾偱偁傜傢偟偰偔偩偝偄丅
夝摎崱夞偺恾偼丂幚偼偲偭偰傕惓妋偱偡(*^_^*)
戞43夞丂 嶼悢栤戣丂乮8寧5擔乣9寧4擔乯丂
壓偺恾偺傛偆偵AB=AC=8cm丂BC=6cm偺擇摍曈嶰妏宍偑偁傝傑偡丅
曈AB忋偵丂AD=5cm丂曈BC忋偵CE=2cm偲側傞揰D,E傪偲傝傑偡丅
AE偲CD偺岎揰傪P偲偡傞偲偒丂AP:CP傪娙扨側惍悢斾偱偁傜傢偟偰偔偩偝偄丅

夝摎崱夞偺恾偼丂幚偼偲偭偰傕惓妋偱偡(*^_^*)

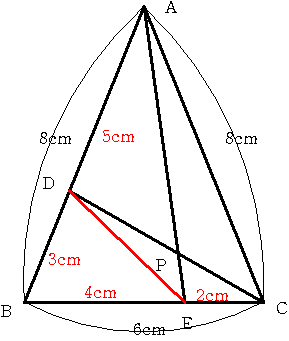
仮BDE偺柺愊傪12偲偡傞偲丂仮CDE偺柺愊偼俇
仮BCD偺柺愊偼18偲側傞偐傜丂仮ACD偺柺愊偼30
傛偭偰AP:PE=仮ACD:仮CDE乮CD傪掙曈偲峫偊偨乯=30:6亖5丗1乧嘆
摨條偵仮ADE偺柺愊偼20丂仮ABE偺柺愊偼12+20=32丂偱偁傞偐傜
仮AEC偺柺愊=16偲側傞
傛偭偰丂DP:PC=仮ADE:仮ACE乮AE傪掙曈偲峫偊偨)=20:16=5丗4乧嘇
丂丂丂丂丂丂丂丂丂儊僱儔僂僗偱傕弌傞偗偳丂偙偆傗偭偰傕弌傞偙偲偵嵟嬤婥偑偮偄偨乮抶偄丠乯
丂丂丂丂丂丂丂丂丂愢柧偺偨傔偵彂偄偨偗偳妏B=90搙偺怳傝傪偡傞偲
丂丂丂丂丂丂丂丂丂仮ADE=1/2亊5亊4丂仮ACE=1/2亊2亊8丂傛傝20:16偺傛偆偵偡偖弌傞偺偱婥偵擖偭偰偄傞丅
仮ABE偲仮CBD偱
AB:BE=8:4=2:1丂CB:BD=6丗3亖2丗1丂妏ABE=妏CBD乮摨偠妏乯傛傝丂仮ABE偲仮CBD偼憡帡偱憡帡斾偑丂8:6=4:3
傛偭偰丂AE:CD=4丗俁乧嘊
AE=1偲偡傞偲丂嘆偐傜丂AP=5/6
嘊偐傜丂CD=3/4丂嘇偐傜丂CP=3/4亊4/9=1/3
傛偭偰丂AP:CP=5/6:1/3=5丗2
丂丂丂丂丂丂丂丂丂丂AC=8cm偼幚偼晄梫偱偡丅
丂