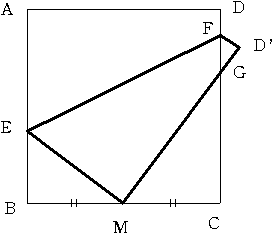
一辺の長さが10cmの正方形で 上の図のように ひとつの頂点Aが対辺の中点Mに重なるように折りました。
このとき CG+GD' の値を求めてください
第42回 算数問題 (7月5日〜8月4日)

一辺の長さが10cmの正方形で 上の図のように ひとつの頂点Aが対辺の中点Mに重なるように折りました。
このとき CG+GD' の値を求めてください
解答
直角三角形MEBの周囲の長さは
BM+ME+EB
=BM+AE+EB
=BM+AB=15cm になっており 周囲の長さの1/3の長さが BMになっていることがわかります。
直角三角形MEB 直角三角形GMC 直角三角形GFD'はすべて相似です。
ここで CG は直角三角形GMCの周囲の長さの1/3
GD' は直角三角形GFD'の周囲の長さの1/3となっていますから
CG+GD' は 直角三角形GMCと直角三角形GFD'の周囲の長さの1/3になります。
その周囲の長さを求めましょう。
GM+MC+CG+GF+FD’+D'G
=GM+GD'+CG+GF+FD+MC
=10+10+5=25
よって CG+GD' =25/3
ところでEB や EMの長さを実際に出してみると...
なんと 三角形EBMは3:4:5の直角三角形になっているではありませんかっ
知らなかったこんなところにこんなものが出来るなんて...世間は狭いですね
BM=6cmにすると 答えが整数にあんるのですが
この3:4:5の三角形を残しておくために 中点の設定にしておきました。
さて 出来た方は 算数によって EBの長さを出してみてください
どのようにすると出るのでしょうか
(FDを求めるのを今回の出題とするか 迷いました)