第38回　 問題　（3月5日〜4月4日）　

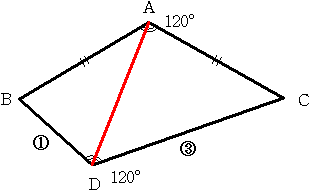
AB=AC ∠BAC=∠CDB=120°　　DB:DC=1:3の四角形があります
四角形ABCDの面積が　220cm^２であるとき　三角形ABDの面積はいくらになるでしょうか。




解答

この四角形を　Aを中心に120°だけ左右に回転した図形を描くと　図のような六角形を得る。
その六角形の�Bの長さの辺を延長し　その交点を　P,Q,R　とすると三角形PQRは正三角形となる。

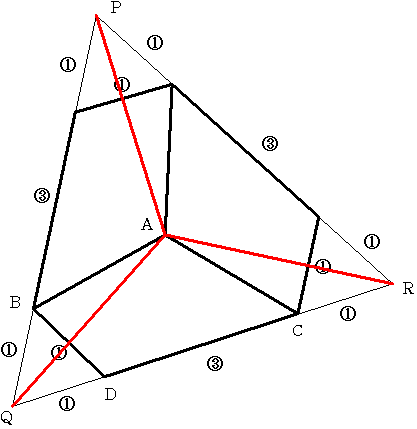
四角形ABCDの面積は220cm^２であるから　六角形の面積は　220×３=660cm^２
正三角形PQRの面積は　660×25/22=750cm^２

三角形AQRの面積は　750×1/3=250cm^２
三角形ADCの面積は　250×3/5=150cm^２
よって　三角形ABDの面積は　220-150=70cm^２となります。

解答　なかさん


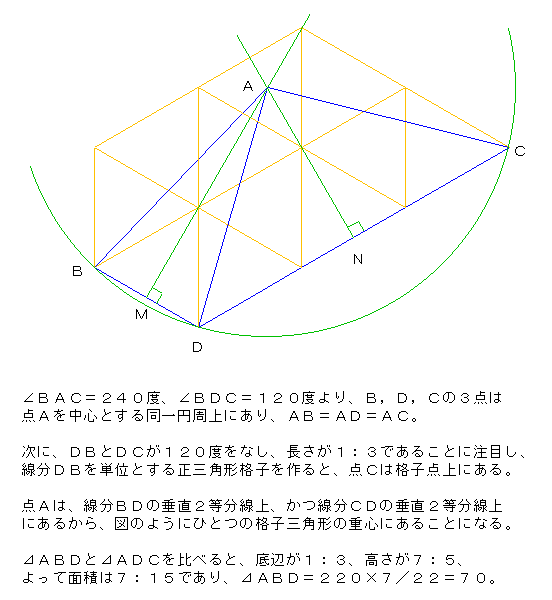
解答　余弦定理を使う　nobuさん　ゴンともさん
点Aを中心とする円周上に点B,D,Cはあります。
AB=ｘ、BD=ｙとすると
BC=√3ｘ

y^2+(3y)^2-2*y*3y*cos120°=(√3x)^2
y^2/x^2=3/13

cos∠BAD=(x^2+x^2-y^2)/2*x*x
cos∠DAC=(x^2+x^2-(3y)^2)/2*x*x

sin∠BAD:sin∠DAC=√(1-(23/26)^2):√(1-(-1/26)^2)=7:16

解答　uchinyanさん

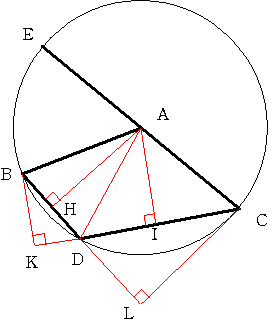
まず、CA を A の方に延長して点 E を AE = AB となるように取ります。
∠BAE = 60度より、△ABE は正三角形で、∠AEB = 60度となり、
∠AEB + ∠BDC = 60 + 120 = 180度で、□EBDC は点 A を中心とする円に内接します。
そこで、AB = AC = AD になります。
次に、A より BD に下ろした垂線の足を H とし、
CD を D の方に延長して B から下ろした垂線の足を K とします。
∠BAH = 1/2 * ∠BAD = ∠BCD なので、二つの直角三角形 △ABH と △CBK とは相似になります。
∠BDK = 60度より、CK = CD + DK = 3 * BD + 1/2 * BD = 7/2 * BD に注意すると、
AB/AH = CB/CK、AH = AB * CK/CB = 7/2 * BD * AB/CB となり、
△ABD = 1/2 * BD * AH = 7/4 * BD * BD * AB/CB。
さらに、A より CD に下ろした垂線の足を I とし、
BD を D の方に延長して C から下ろした垂線の足を L とすると、
△CAI と △CBL とは相似になり、全く同じようにして、
△ACD = 1/2 * CD * AI = 5/4 * CD * BD * AC/BC。
そこで、AB = AC、CD = 3 * BD より、△ABD : △ACD = 7 : 5 * 3 = 7 : 15 になります。
したがって、△ABD = 7/(7+15) * □ABDC = 7/22 * 220 = 70 cm^2。