Dチームと Pチームが試合をしました。先に6勝したほうが勝ちです。
第1問
(1) Dチームが6勝して勝った
(2) Dチームは連敗したことがある(何回そういうことがあったかは不明)
(3) Dチームは最大で2つ負け越していたときがある(何回そういうことがあったかは不明) 3つ以上は負け越していないということ
このような条件の下でDチームが勝つのは何通りありますか。
第2問
(1) Pチームが6勝して勝った
(2) Pチームは最大で2連敗したことがある(何回そういうことがあったかは不明) 3連敗以上はしていないということ
(3) Pチームは最大で2つ負け越していたときがある(何回そういうことがあったかは不明) 3つ以上は負け越していないということ
このような条件の下でPチームが勝つのは何通りありますか。
解答
問題1
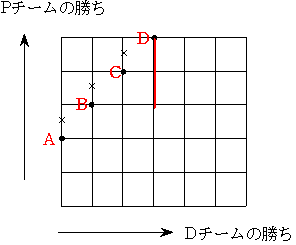 図のように考えます
図のように考えます×は通れない道 黒丸のどれかは必ず通るということです。
たとえば Dで初めて2つ負け越すとすると その前の2試合では連敗していることがわかります
(図の赤い線がそうです)
同様に Cで初めて2つ負け越すとすると その前の2試合では連敗しています
Bで初めて2つ負け越すとするとその前の2試合では連敗しています。
Aで初めて2つ負け越すとすると その前の2試合では連敗しています。
つまり (3)の条件をみたすときは かならず(2)の条件を満たしていることがわかります。
よって 左下から右上に進む時に A,B,C,Dの少なくとも1点を通る場合の数を求めるとよいことになります
それは 全体から A,B,C,Dを通らない時を引けばいいわけですから
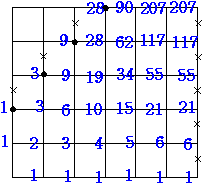
全体の場合の数
207+117+55+21+6+1=407通り
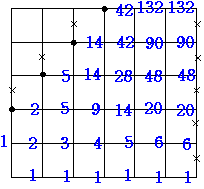
A,B,C,Dを通らない場合の数
132+90+48+20+6+1=297通り
よって 407-297=110通り となります
問題2
問題1の解答を利用して
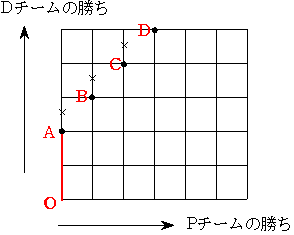 図のように考えます今度は110通りのうち3連敗以上している場合の数を除きます
図のように考えます今度は110通りのうち3連敗以上している場合の数を除きます3連敗以上するのは 5つの縦の線上のどこかで生じます

1の線の場合は 負負でAの点まで進み 勝勝勝勝勝 このあと赤い線をたどって 負負負 勝 しかありません
1通り
2の線の場合は 負負でAの点まで進み 勝勝勝勝 このあと赤い線をたどって 負負負 勝勝 しかありません
1通り
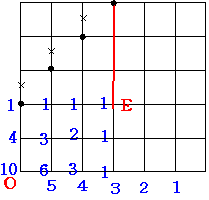
3の線の場合は 最終的には図のEから3連敗します。
EからOまでもどる道は 10通りです。
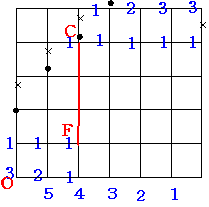
4の線 の場合その1
FからCまで3連敗以上しているとき
3×4=12 通り

4の線の場合その2
上で数えていない場合の道順
1通り

5の線の場合その2
14通り
以上から 3連敗以上しているのは
1+1+10+12+1+14=39通り
よって答えは 110-39=71 通り
問題2の別解
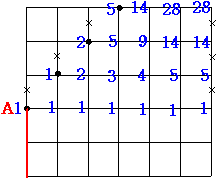
 たとえばこのような場合です このようなものが 3通りありますから
たとえばこのような場合です このようなものが 3通りありますから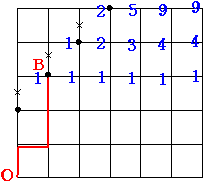 Bのとき
Bのとき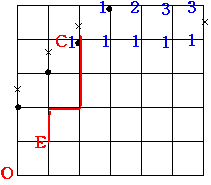 Cのとき
Cのとき