第35回　 問題　（12月5日〜1月4日）　


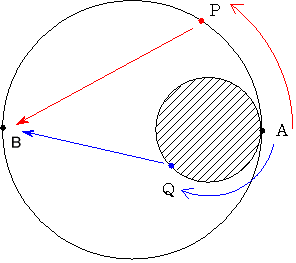
円形のサイロの周りを一周する道が２つあります。　１つはサイロのすぐ外側にあり　
もうひとつはサイロにA地点で接する一周　6280m　の円形の道です。
P君とQ君が同時にA地点から出発して　
P君は大きな円の道を半時計まわりに　
Ｑ君はサイロの回りの円の道を時計まわりに一定の速さで一周します。
大きな円の道を　3140m　進んだ地点Bに旗が立っていて　P君もQ君も出発してから
15分後に　初めてこの旗を見ることができました。
P君が一周するのに１時間10分かかったとします。

(1)P君とQ君のどちらが先に一周したでしょうか
(2)2人が一周するのにかかった時間の差は何分でしょうか
　　　　

解答

Qが時計回りに進んだとしても15分でB地点が見える　そのときのB,Q,Pの位置は下図の通り

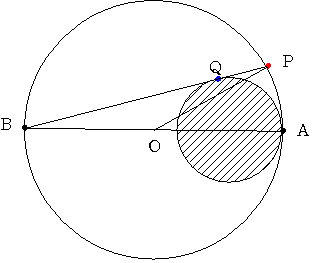
このとき　Pは一周するのに70分かかるので　ABを進むのに35分　PBを進むのに35-15=20分
弧AP:弧PB=15:20=3:4
大きい円の中心をOとすると　角BOP=180°×3/7
これは二等辺三角形OPBの外角であるから　角ABP=90×3/7

小さい円の中心をRとすると
三角形BQRに着目すると　角ARQ:角QRB=(90+90×3/7):(90-90×3/7)=(1+3/7)：(1-3/7)=10：4＝5：2
よって　Qが一周するのにかかる時間は　15×14/5=42
70-42=28分

答　Qが28分早く一周する