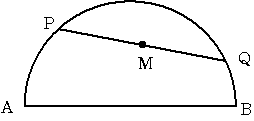
上の図のように 直径ABの長さが12cmの半円があります。この円弧AB上に2点P,Qをとり線分PQの中点(真ん中の点)を
Mとします。点Pと点Qをいろいろ変えたときに 点Mが存在できる領域の面積を求めてください。
必要なら円周率を3.14として計算してください。
第30回 問題 (6月9日〜7月4日)

上の図のように 直径ABの長さが12cmの半円があります。この円弧AB上に2点P,Qをとり線分PQの中点(真ん中の点)を
Mとします。点Pと点Qをいろいろ変えたときに 点Mが存在できる領域の面積を求めてください。
必要なら円周率を3.14として計算してください。
解答
1 まず 円全体で Pを固定して Qを円周上を一周させたときに Mの軌跡はどうなるか考えます
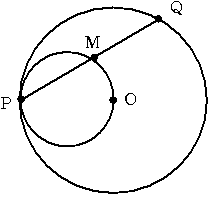
Pを中心とする相似の縮小になるので 図のように O P を直径とする円を描くことがわかります
2 次に半円ではどうなるか考えます

Pを固定してQをPからBまで移動すると MはOPを直径とした円周上を動きますがQはBでストップし
Mは 図の2つの円の交点Nでストップします。
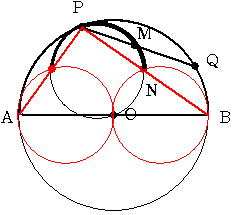
QがPからAまで移動したときも同様です。ですからMの存在範囲は上の円弧の部分となります。
3 Pが動くと この円弧も動きます
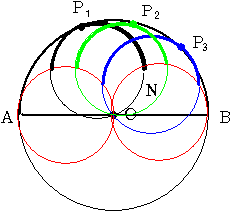
4 以上から 点Mの移動できる領域は
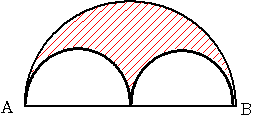
上のようになるので
1/2×6×6×3.14-3×3×3.14=9×3.14=27.26 となります
別解 中学の知識を使って

上の図のように補助線を引きます
点Pについてだけ考えると
角OMP=90度より 角AMO<90度 つまりMはOAを直径とする半円の外であることがわかります
逆にOAを直径とする円の外に点Nをとるとき 角ONA<90度 より 角ONP=90度となるように
点Pを弧AB上にとることができる。
つまりMはOAを直径とする半円の外にある任意の点となる。
点Qについても同様に考えると Mの存在範囲は上の解の4で示された領域になることがわかります。