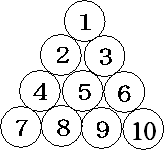
上の図のように三角形状に円が並んでいて その円の中には規則的に数字が書かれています。
(数字の書いてある円は下のほうにずーっと並んでいます)
このときある円の周りには6個の円があって その円に書かれている6個の数の和が98765432となっていました。
このとき 6つの円に囲まれたまん中の円に書かれている数はいくらでしょうか。
たとえば 上の図で 5の周りには2 3 4 6 8 9の数が書かれた円があり その数の和は 32となっています。
第29回 問題 (5月5日〜6月4日)

上の図のように三角形状に円が並んでいて その円の中には規則的に数字が書かれています。
(数字の書いてある円は下のほうにずーっと並んでいます)
このときある円の周りには6個の円があって その円に書かれている6個の数の和が98765432となっていました。
このとき 6つの円に囲まれたまん中の円に書かれている数はいくらでしょうか。
たとえば 上の図で 5の周りには2 3 4 6 8 9の数が書かれた円があり その数の和は 32となっています。
解答
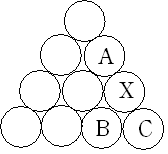
(1)最初に列の右端の数字の関係を考えます。上のように
ある列の右端の数をA、その下の右端の数をX、さらにその下の列の数を右からB,Cとします。
Xの列の個数 と B,Cが書かれている列の左端からBまでの個数が等しいことから AとBの真ん中の数がXであることから
AとBの和はXの2倍であることがわかります。
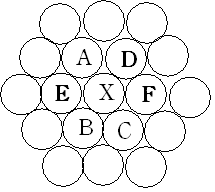
(2)次にたくさん並んだ数字の中のある数字Xが上のように6つの数字でかこまれているとします。
AとXとBの位置関係は(1)でのAとXとBの位置関係と同じです。というのは(1)のA,X,Cを右に1つづつ
ずらしたことになるからです。つまりここでもAとBの和はXの2倍となります。
よって AとCの和はXの2倍より1大きく BとDの和もXの2倍より1大きいことがわかります。
また 明らかに EとFの真ん中の数がXですからEとFの和はXの2倍となっています。
以上のことからXの周りの数の和は Xの6倍より2大きい数になりますから
xの数は (98765432-2)÷6=16460905であることがわかります
(3)
さて 実際に16490905が真ん中にあり 両端にないことを調べなくてはいけません。
このあたりの検証を算数でやってみましょう
1からnまでの和が n(n+1)/2ですから 16460905の2倍の32921810がn(n+1)になるかどうかです。
n(n+1)をn^2に近似して 5500付近から大雑把に検討すると
5500^2=30250000 5600^2=31360000 5700^2=32490000 5750^2=33062500
5740^2=32947600
5739*5740=32941860
5738*5739=32930382
5737*5738=32918906
となるので 16460805は 5738列目の途中の数であることがわかります。