一辺が1cmの正方形を底面とし 高さが異なる直方体がいくつかあります。これを横に一列に
並べて左(それらが重なる方向)から見ると見える直方体はいくつあるか考えます。
たとえば 高さが 1cm 2cm 3cm 4cmの4つの直方体を 2cm 1cm 4cm3cmの
順に並べ左から見ると 高さ1cmと3cmの直方体は見えず 高さ2cm4cmの直方
体の側面が見えます。
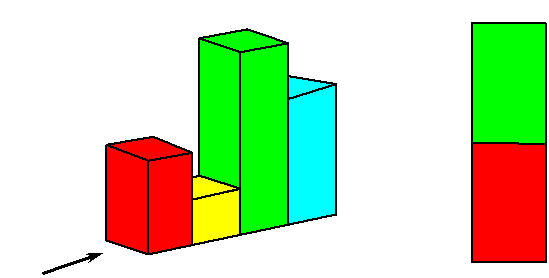
では 高さが異なる10個の直方体を一列に並べて横から見たとき 側面が5つだけ
見えるような直方体の並べ方は何通りあるでしょうか
たとえば 高さ1cm 2cm 3cm 4cm の直方体のとき2個の直方体が見えるような
並べ方は
1423 1432 2143 2413 2431 3124 3142 3214 3241
3412 3421 の 11通りあります。
yanさんの解答
10C6×5!+10C5×5C2×4!+10C4×6C3×3!×2!
+10C4×6C2×4C2×3!/2! +10C3×7C3×4C2×2!×2!/2!
+10C3×7C2×5C2×3C2×2!/3!+10C2×8C2×6C2×4C2/5!
=269325
ほげの解答
n個の直方体を並べたときにk個の側面が見えるような並べ方をa(n,k)通りとします。
このa(n,k)通りの並べ方は大きく2つに分けられます。一番右に一番高い直方体があるときと
そうではないときです。
一番右に一番高い直方体があるような並べ方は
一番右の直方体をとり除くと n-1個を並べたときにk-1個見える並べ方と同じだけの
場合の数があります。 これはa(n-1,k-1)通りになります。
一番右に一番高い直方体がないときの並べ方は
一番右の直方体は n-1通りあります。これを取り除いたn-1個の直方体を左から見ると
k個の側面が見えるので (n-1)×a(n,k)通りあります。
すると a(n,k)=a(n-1,k-1)+(n-1)×a(n-1,k)であることがわかります。
これで 順に n=1の時から 10までを求めたのが下の表です。 縦がn 横がkとなっています。