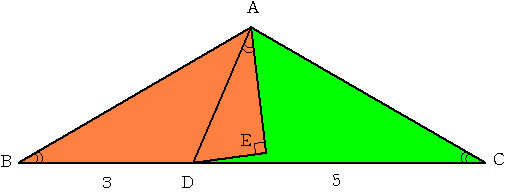
図のように三角形ABCは二等辺三角形で 角ABC=角ACB=30度
三角形ADEは直角三角形で 角DAE=30度 角AED=90度となっています。
また Dは辺BC上にあり BD:DC=3:5とします。
このとき
四角形ABDEと四角形AEDCの面積比をもっとも簡単な整数比であらわしてください。
解答 67:61
第24回 問題 (12月5日〜2月4日)

図のように三角形ABCは二等辺三角形で 角ABC=角ACB=30度
三角形ADEは直角三角形で 角DAE=30度 角AED=90度となっています。
また Dは辺BC上にあり BD:DC=3:5とします。
このとき
四角形ABDEと四角形AEDCの面積比をもっとも簡単な整数比であらわしてください。
解答 67:61
この問題は 先に算チャレで C-Dさんが解いた正8角形を使う解法に感動して作りました。
算チャレで出てから日がたっていないので またか と思う方がいらっしゃるかも知れないので
数ヶ月おいてから ということもあったのですが 待ちきれないので 出題いたしました。(*^_^*)
もちろん三平方で解くことも可能ですね。
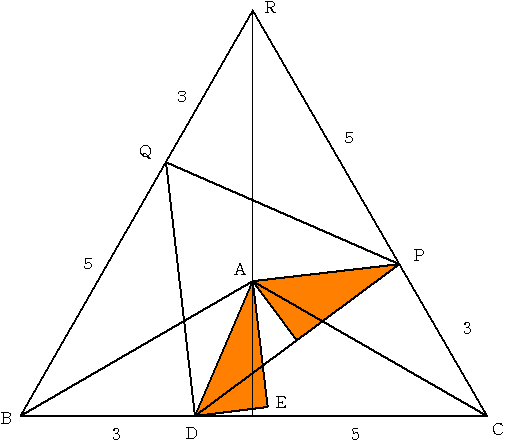
この図形をAを中心に120度 左右に回転すると 正三角形BCRができます。
このとき問題の四辺形ABDEを2つの三角形に分けて面積を求めます。
正三角形BCRの一辺の長さを8とし、一辺が1の長さの正三角形の面積を1とします。
三角形ABDの面積
三角形ABCの面積は正三角形BCRの面積の1/3なので 1/3×8×8=64/3
三角形ABDの面積は更にその3/8なので64/3×3/8=8
三角形ADEの面積
三角形DPQの面積は正三角形BCRから3つの三角形を切り落としたもので
8×8-3×3×5=19
三角形ADEの面積は この正三角形の1/6であることが上の図からわかる(茶色の三角形の面積は同じ)
よって 19/6
このことから四辺形ABDEの面積は 8+19/6=67/6 四角形AEDCの面積は 64/3-67/6=61/6
面積比は67:61