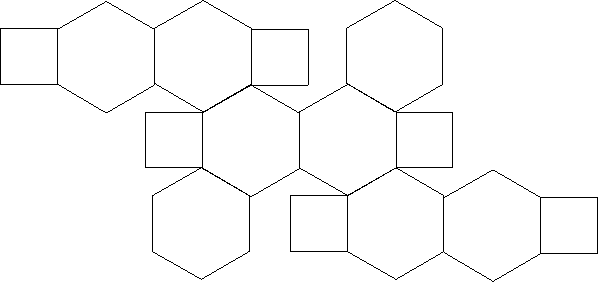
下の展開図のように8つの正六角形と6つの正方形で囲まれた立体図形
があります。正方形の面積が72cm^2のとき この立体の体積を求めてください。
解答
この立体は展開図から組み立てて下のように立方体にはめ込むことができます。
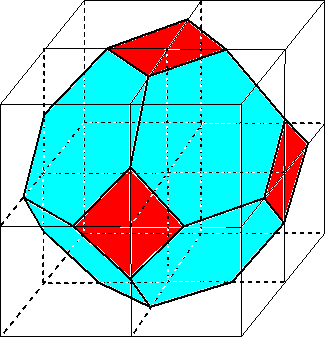
この立方体を8つの小立方体に切ると一つ一つは下のような図形であることがわかります。
第23回 問題 (11月5日〜12月4日)
下の展開図のように8つの正六角形と6つの正方形で囲まれた立体図形
があります。正方形の面積が72cm^2のとき この立体の体積を求めてください。

解答
この立体は展開図から組み立てて下のように立方体にはめ込むことができます。

この立方体を8つの小立方体に切ると一つ一つは下のような図形であることがわかります。
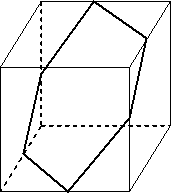
これは 立方体を切断したときに断面が正六角形になるきり方で 断面は立方体の中心を通っています。
つまり体積は2等分されます。
よって求める体積は大きな立方体の半分になります。
赤い正方形の面積は大きな正方形の1/8の面積ですから大きな正方形の面積は72×8=576cm^2
おおきな立方体の一辺は 24×24=576から 24cm
求める体積は 24×24×24÷2=6912cm^2
解答2
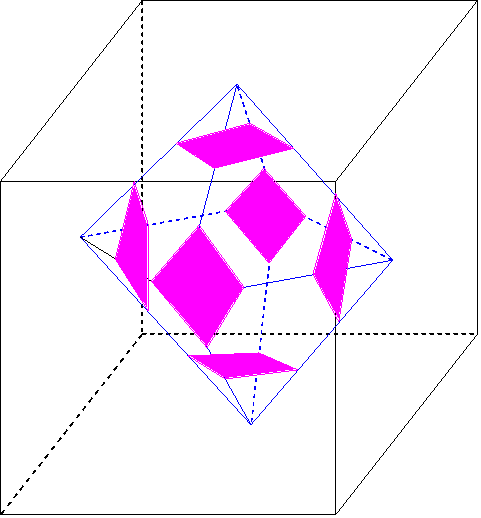
この立体は正8面体から6つの四角錐を切り取ったものとなっている
正面からみると

一番中にある正方形の面積が72cm^2なので2番目に大きな正方形の面積は
72×3×3 そして一番大きな正方形の面積は 72×3×3×2
よって正方形の一辺の長さは 12×3=36cm
この中に入る正8面体の体積は 底面積が1/2の錘なので
36×36×36×1/2×1/3=36×36×6
切り取る四角錘1つの体積はこの体積の1/2の(1/3)^3倍なので
1/2×1/27×6=1/9
求める体積は元の体積の8/9なので
36×36×6×8/9=6912cm^3となります。