第20回　 問題　（8月5日〜9月4日）

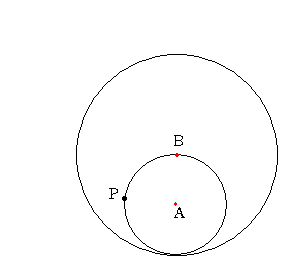
下の図のように大きい円Bとそれに内接している小さい円Aとがあります。
円Aの半径は12cm　円Bの半径は24cmです。円Aが円Bに接しながら滑ら
ずにもとの位置にくるまで回転すると、円Aの円周上の点Pがすすむ
道のりはいくらでしょう。

解答
問題を少々変えて図の位置にPがあるところから考えるといいと思います。

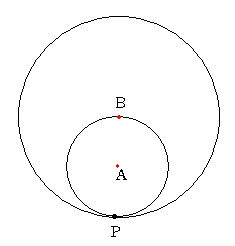
上の図から円Aが中心角θだけ回転したと想定します

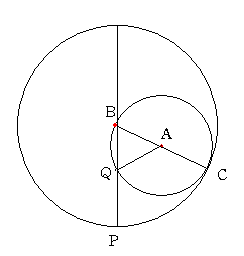
Pが上の図の大きな円の直径上を動く事を証明します。
図のように直径と円Aの交点をBとQとします。
円の大きさの比が1:2であることから∠CBP=θ/2であることがわかります。
このとき三角形ABQは二等辺三角形ですから角QACはθとなります。
つまり点Qは点Pに他ならない事がわかります。
以上から点Pは直径上を動く事がわかります。

円Aが一周するときはPは一往復するので　みちのりは　24×2×2=96cmとなります。