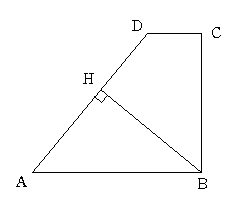
曈DC偺挿偝偼曈AB偺挿偝偺敿暘偱偡丅
嶰妏宍ABC偼捈妏擇摍曈嶰妏宍偲側偭偰偄傑偡丅
B偐傜曈AD偵悅慄傪壓傠偟偦偺懌傪H偲偟傑偡丅
偙偺偲偒BH偼懳妏慄BD偺挿偝偺壗攞偲側偭偰偄傞偱偟傚偆偐丅
戞14夞丂 栤戣丂乮2寧5擔乣3寧4擔乯
曈AB偲曈DC偑暯峴側戜宍偑偁傝傑偡
曈DC偺挿偝偼曈AB偺挿偝偺敿暘偱偡丅
嶰妏宍ABC偼捈妏擇摍曈嶰妏宍偲側偭偰偄傑偡丅
B偐傜曈AD偵悅慄傪壓傠偟偦偺懌傪H偲偟傑偡丅
偙偺偲偒BH偼懳妏慄BD偺挿偝偺壗攞偲側偭偰偄傞偱偟傚偆偐丅

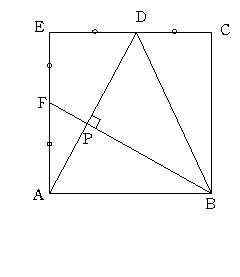
夝摎丂壓偺恾偺傛偆偵惓曽宍偺2偮偺曈CE,AE偺拞揰D,E寢傇帪偵岎揰P偑
幚偼忋偺恾偺揰H偵側偭偰偄傞偙偲偑傢偐傝傑偡丅
忋偺恾偺H傪壓偺恾偺P偱撉傒曄偊偰撉傫偱偔偩偝偄丅
偙偺偲偒丂憡帡側捈妏嶰妏宍偨偔偝傫尒偮偐傝傑偡偑丄偦偺捈妏傪偼偝傓俀曈偺斾偼1:2偱偡偐傜
嶰妏宍APF偱PF=侾偲偡傞偲丂AP=2丂
嶰妏宍EPA偱丂AP=2傛傝丂BP=4
BD=BF=4+1=5偲側傝傑偡偐傜丂BH偼懳妏慄BD偺4/5攞偲側傝傑偡丅
強偱丄偙偺偲偒DP=AD-A=5-2=3偲側傝傑偡丅
嶰妏宍BPD偼3:4:5偺捈妏嶰妏宍偵側偭偰偄傞傫偱偡傛偹丂傃偭偔傝偟傑偟偨丅(~_~;)
暿夝丂
AB=2偲偟傑偡
嶰妏宍ABD=1/2亊2亊2=1/2亊AD亊BP偐傜丂AD=AB=併5傪戙擖偟偰
BP=(係併5)/5丂傛傝丂BP=4/5BD偲側傝傑偡丅
Banyanyan偝傫偺夝摎丂恾宍偼摨偠張棟傪偟偰傑偡偑偦偺屻偺斾偺弌偟曽偑偄偄側偁
偲巚偭偨偺偱宖嵹偄偨偟傑偡
俠俢傪墑挿偟偰丄俙偐傜俠俢偵悅慄傪壓傠偟丄偦偺懌傪俤偲偡傞偲
巐妏宍俙俛俠俢偼惓曽宍偱偁傞丅
仮俙俢俤偲仮俛俢俠偼崌摨乮徹柧棯乯丅傑偨丄
佢俤俙俫亄佢俫俙俛亖佢俫俙俛亄佢俫俛俙亖俋侽亱丄佢俤亖佢俙亖俋侽亱傛傝丄
仮俛俥俙傕崌摨丅仮俛俙俫偼憡帡丅
俙俥亖俤俢亖俠俢亖侾乛俀俙俛
俛俥亖俙俢亖俛俢
夝偒曽嘆
俛俫丗俥俫亖仮俙俛俢偺柺愊丗仮俙俥俢偺柺愊亖惓曽宍俙俛俠俢亊侾乛俀丗惓曽宍俙
俛俠俢亊侾乛俉亖係丗侾
傛偭偰丄俛俫亖俛俢亊係乛俆
夝偒曽嘇
俙俫丗俛俫亖俠俢丗俛俠亖侾丗俀
俙俫丗俢俫亖仮俙俛俥丗仮俛俥俢亖惓曽宍俙俛俠俢亊侾乛係丗惓曽宍俙俛俠俢亊俁乛
俉亖俀丗俁
傛偭偰丄俛俫丗俛俢亖俀亊俀丗俀亄俁亖係丗俆
彫悪尨 孾偝傫偺夝摎丂恾傪偐偐側偔偰偛傔傫偹丂偙偺夝朄偼婥偑晅偒傑偣傫偱偟偨
曌嫮偵側傝傑偡偹m(__)m
俛俢亖俙俢丅俙俢丆俛俠傪墑挿丅岎揰傪俤偲偍偔丅嚈俙俛俫佷嚈俙俤俛佷嚈俛俤俫丅
傑偨丄俙俛丗俛俤亖侾丗俀傛傝丄俙俫丗俛俫丗俤俫亖侾丗俀丗係丅
俛俫丗俙俤亖俀丗俆丏俛俢亖1/2俙俤傛傝丄俛俢丟俛俫亖俆丗係
Banyanyan偝傫偺夝摎俀
彫悪尨偝傫偺墑挿偺傾僀僨傾傪僷僋偭偰傒傑偟偨丅
傑偀丄扨側傞憡帡側傫偱偡偑丒丒丒
俛俫偵暯峴側慄暘俹俻傪恾偺倃偐傜倄傑偱摦偐偟偰傒傑偡丅
偙偺偲偒丄慄暘俹俻乮挿偝傪俴偲偍偔丅傕偪傠傫俛俢亖俴偱偡丅乯
偺偆偪丄俙俢傛傝塃懁偵偁傞晹暘偺挿偝傪倶偲偡傞丅
俹偑倃偵偁傞偲偒丄倶亖俴
俹偑倄偵偁傞偲偒丄倶亖侽
偙偙偱丄俹偑俛偵偁傞偲偒傪媮傔傟偽傛偄偐傜丄
俛俫亖乮俴亅侽乯亊俛倄乛倃倄亖係乛俆俴
傎傫偲偆偼偙傫側偙偲偟側偔偰傕丄仮俙倃倄佷仮俫俛倄偱嵪傫偱偟傑偆傫偱偡偑丒丒
拞妛柪扵掋偝傫偺夝摎
偦偺侾
仮ABH偲仮DBC偼憡帡側偺偱BH丗BC=AB丗BD,丂偟偨偑偭偰BH*BD=AB*BC
椉曈傪BD*BD偱妱傞偲BH/BD=AB*BC/BD*BD=2*2/乮2*2+1乯亖4/5
偦偺俀
仮BCD偺捀揰C偐傜曈BD偵偍傠偟偨悅慄偺懌傪E偲偟傑偡丅
仮AHB偲仮CEB偼崌摨丄仮CEB丄仮DEC丄仮DCB偼憡帡偱偁傝丄DE丗EC亖EC丗EB=DC丗CB=1
丗2丅
DE=1偲抲偔偲EC=2,EB=BH=4丄DB=DE+EB=5
傛偭偰BH丗BD=4丗5丂偱偡丅丂丂丂丂丂丂拞妛柪扵掋
傒側偝傫偺僐儊儞僩廤
A(0丄0)丄B(2丄0)丄D(1丄2)偲偍偔偲丄H偺嵗昗偼丄乮2/5丄4/5乯偱丄偁偲偼丄
BH**2=乮4/5乯**2*5亖乮4/5乯**2*BD**2BH=4/5*BD
嶰暯曽偱傗偭偪傖偭偨両丂仺巹偼偙傟偱妋擣偟傑偟偨
柺愊偺娭學偐傜夝偒傑偟偨丅
尦偺恾宍偑惓曽宍偱偁傞偙偲偼偡偖偵暘偐偭偨偺偱丄偁偲偼椺偵傛偭偰
俁丗係丗俆偺捈妏嶰妏宍傪嶌傝傑偟偨丅乮偲偄偆傛傝丄偱偒傑偟偨偲尵偭偨曽偑惓偟偄偱偡偑...丅乯
寢峔丄擸傫偱偟傑偄傑偟偨丅
3:4:5偺捈妏嶰妏宍偵偼婥偯偒傑偣傫偱偟偨丅偱傕憡帡斾偱(憡帡偼嶼悢?偱偟偨偭偗)
側傫偲偐夝偗傑偟偨丅暿夝偺傛偆偵悢妛偩偲偝偡偑偵堈栤偱偡偹丅
偙傫偽傫偼両両拞妛庴尡偺帪婜偩偗偵丄幚尡偡傞偙偲偱丄壗偐偵婥晅偒丄壖愢傪棫偰丄
岞幃傪嶌偭偰傒偰丄傕偆彮偟戝偒側悢帤戙擖偟偰傒偰丄丄丄偄偗傞偧両両偲偄偆弖娫偑
嵟崅偵偆傟偟偄偱偡丅偄偮傕丄妝偟偔丄偨傔偵側傝丄夝偒偑偄偺偁傞椙栤偵姶幱偟偰偍傝傑偡丅
仺幚尡壖愢専徹丂偲偄偆偺偑壢妛幰偲偟偰偺婎杮偱偡偹(~o~)
嶼悢偱偼夝偗偰偄傑偣傫丂仺嶼悢偱傕傗偭偰傒偰偔偩偝偄^_^;
朲偟偄偺偱丄嵗昗寁嶼偱曅晅偗傑偟偨丅 (^^;仈朲偟偔側偔偰傕偦偆傗偭偨偵堘偄側偄乧
AD偺墑挿慄偲BC偺墑挿慄偺岎揰傪E偲偡傞丅俁妏宍EAB傪峫偊傞丅屻偼崌摨偲憡帡丅
BC偲AD傪墑挿偟偰傒傞偲丄憡帡側捈妏嶰妏宍偑偨偔偝傫尰傟偰乧偲偟偰傒傑偟偨丅1:2:
儖乕僩5偺嶰妏宍偲3:4:5偺嶰妏宍偺娭楢惈偲偄偊偽丄慜幰偺彫偝偄曽偺塻妏丗屻幰偺
戝偒偄曽偺塻妏亖侾丗俀偁偨傝偱偟傚偆偐丅偙偆峫偊傟偽丄崱夞偺栤戣偵3:4:5偺嶰妏宍偑
尰傟傞偺傕僫僢僩僋丠
嶐擔丄悢妛栤戣傪夝摎偟偨屻丄乽拞妛傊偺嶼悢乿偺弌戣擔偱偁傞偙偲傪巚偄弌偟丄偦偪傜偵
堏摦丅傕偆嶼悢栤戣偺曽偼偡偭偐傝朰傟偰偄傑偟偨丅愄偼乽傾儖拞僴僀儅乕乿偩偭偨偺偑
崱偱偼棫攈側乽傾儖僣僴僀儅乕乿乽儃働乿偵側傝偮偮偁傝傑偡丅
嶰暯曽偺掕棟偲嶰妏宍偺憡帡傪巊偭偰夝偒傑偟偨丅
憐掕夝偺傛偆偵曗彆慄傪堷偄偰峫偊傑偟偨丅惓曽宍偲偄偆偙偲偼愭廡偺嶼僠儍儗傕偁偭偨
偣偄偐偡偖偵傢偐傝傑偟偨乮丱丱丟
嶰暯曽偱夝偄偪傖偄傑偟偨偑丄柾斖夝摎傪尒偰丄傕偆彮偟擲傟偽椙偐偭偨偲巚偄傑偟偨丅
惓曽宍偲憡帡偱偱偒傑偟偨丅彫悪尨偝傫偲摨偠曽朄偱偟偨丅庴尡僔乕僘儞偑偒傑偟偰丄
彮偟朲偟偔偟偰偄傑偟偰丄偡偭偐傝丄朰傟偰偄傑偟偨丅崱擭傕傛傠偟偔偍偹偑偄偟傑偡丅