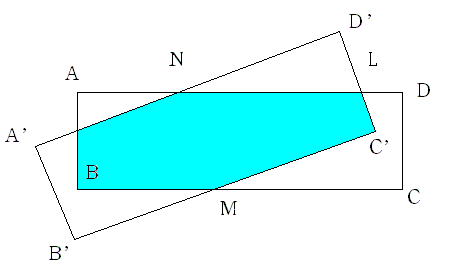
ADとA'D'の交点をNとするとAN=12cmでした ADとD'C'の交点をLとするとLD=9cmでした。このとき2つの長方形の重なった部分(図の濃い水色の部分)の面積を求めてください。
第10回 問題 (9月5日〜10月4日)
 |
横BCの長さが縦ABの長さの半分の長方形ABCDがあります。辺BCのまん中の点Mを中心にこの長方形を回転させた長方形をA'B'C'D'とします。 ADとA'D'の交点をNとするとAN=12cmでした ADとD'C'の交点をLとするとLD=9cmでした。このとき2つの長方形の重なった部分(図の濃い水色の部分)の面積を求めてください。 |
なぜ図を不正確に書いたかというと...すぐに長さの関係がわかってしまうからです(~o~)
当初 説明が間違っていて申し訳ありませんでした。m(__)m
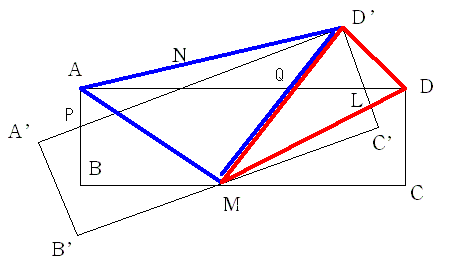 |
LD=LD'=9cmであることの証明 三角形MDD'は二等辺三角形なので角D'DM=角DD'M 角MDL=角MD'L=45度より角D'DL=角DD'L 三角形DD'Lが二等辺三角形となり LD'=LD=9cm ND'=NA=12cmであることの証明 三角形MD'Aは二等辺三角形なので角AD'M=角D'AM 角MD'A'=角MAN=45度より角ND'A=角NAD' 三角形ND'Aが二等辺三角形となり ND'=NA=12cm 直角三角形D'NLが3:4:5より辺LN=15cm AD=12+15+9=36 AB=18 三角形APNと三角形LDNが合同で AP=9 PB=9 LC'=9 C'M=18 BM=18などを 出しておいて 求める面積は 三角形PBM+三角形PMN+三角形NML+三角形LMC' =1/2(9×18+15×18+15×18+9×18) =432 |
巷の夢 さんの解法
図は面倒なので文字のみとしますのでご了承下さい。
BM=CM=AB=CD=RとしMを中心とした半円を長方形ABCDの中に描きます。辺ADへ
点Mからおろした垂線の交点をM'とします。又、長方形A'B'C'D'と辺AB及びADの交点を
P,Qとします。
すると点P,Q,Nは、この半円への3本の接線の交点になります。今、NM'=y、QM'
=xとすると NQ=x+y=15ですから15+12+9=36=2R、因ってR=18、即ち、
x=9、y=6となります。
後は三角形6個の面積ですが、(2x+y)Rですので、各々の値を代入し、43
2が求めるものです。