第9回　 問題　（8月5日〜9月4日）

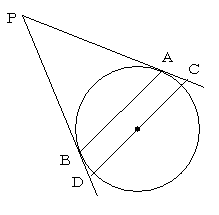
左図のように半径4ｃｍの円に、円の外にある点Pから２本の接線を引きます。接点をA,Bとするとき、ABに平行で円の中心を通る直線と接線の交点をC,Dとします。 AP=8cmのとき、CDの長さはABの長さの何倍でしょうか。

この問題は最初CDを引かずPQ:QOを求めるのが原型でした。それをいろいろ変えているうちに
解答２のような解答が出来る事を考えずに今回の問題を出題してしまいました。
解答を送付していただいて勉強になりました。(~_~)

解答

上の図のように補助線を引きます。
三角形APQと三角形AQOは相似で相似比はAP:AQ=8:4=2:1
面積比は4:1でこの三角形をPQ　OQを底辺と考えて見直すと　高さが同じで面積比が4:1であるから
PQ:QO=4:1
三角形APBと三角形CPDは相似で高さPQとPOの比が4:5となりAB:CD=4:5
CDはABの5/4倍となります。

正解者掲示板には　5b4aで入る事になります。

解答2
三角形OAPと三角形CAOは相似で　OA:AP=CA:AOより　4:8=CA:4　CA=2
三角形ABPと三角形CDPは相似で　AB:CD=AP:CP=8:10=4:5
よって5/4倍です

解答３
三角形OAPで三平方の定理からOP^2=OA^2+AP^2=4^2+8^2=80
OP=4√5
三角形APQと三角形OPAは相似で　PQ:AP=PA:OPより　PQ:8=8:4√5
PQ=16/√５　よってPQ:PO=16/√５:4√５=4:5
三角形ABPと三角形CDPは相似で　AB:CD=PQ:PO=4:5