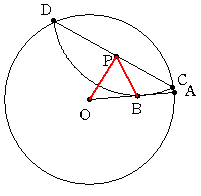
半径5cmの円Oがあります。この円の半径OA上に、OB=3cmとなる点Bをとります。図のように、円OをCDで折り曲げて
折り曲げた弧CDが半径OAとBで接するようにしました。このとき、CD上に点PをとってOP+PBの長さを求めます。
OP+PBが最小になるときの値を求めてください。
解説
いろいろ煙幕をはったんですけどほとんどの人が引っかからなかったようです。接するから垂線だとか、
5,3という数字から3:4:5の直角三角形を連想しないかなあ といった感じです。
実は円周が点Bを通るようにいろいろとCDをかえて折り曲げると、その直線群は楕円を作ります。
この直線群を包絡線といいます。ぜひ円をきりぬいてやってみてください。
そのことをうまく問題に出来ませんでした。
解
こういう問題を解く基本は折り返しですよね。折り返した図形を元に戻して、その先をB’とすると
OP+PB=OP+PB'ですから、最小値はこれが一直線になっているときになります。
よって最小値は半径と同じ5cmという事になります。