第5回　算数問題解答　　　（4月5日〜5月4日）

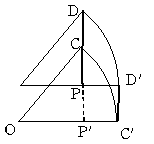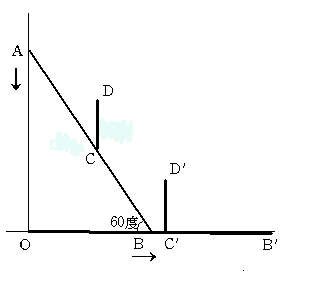
大工のゲンさんはあるとき水平な地面に対して垂直にたっている壁に、まっすぐに12mのはしごをかけました。そのとき図の
角ABOは60度だったそうです。このはしごをABのちょうど真ん中の点まで上ってきたときに、どういうわけかはしごがずりずり
落ちてきて、Aは壁から離れることなくOまで、Bは地面から離れることなくB'まで移動したそうです。
そして、ゲンさんはといえば、さすが　むかしとったきねずか、CDに立っていたゲンさんは、見事C'D'に着地したそうです。
ゲンさんは1.5mの高さで腰は曲がっていません。図はと〜っても不正確で、C'の位置がおかしい等のクレームは受け付けません。
そのほか、算数的に都合よく解釈してください。　さて、このとき
(1)ゲンさんのつま先は　CからC'まで何センチ移動しましたか。
(2)ゲンさんの体CDが通った面積は何m＾2でしょう　（体積ではないです　だからぁ都合よく解釈して、平面で考えるんですってばぁ）

解答

(1)
　ABがどんな位置にあってもCはABの中点ですからOはABを直径とする円周上にあります。
つまり、OC=AB/2=6mで、ゲンさんはOを中心とする半径6mの円周上を動く事になります。
角COB=60度　よって、12×3．14×60/360=6．28m=628cmです。

　直径にたいする円周角は90度って算数の範囲だったよね。ちがったらゴメンなさいm(__)m

(2)

上の図のように考えると、DCC'D'=DP'C'D'-CP'C'C=DP'C'D'-DPD'D=長方形PP'C'D'
から、1/2×6×1．5=4.5mとなります。