��4��@�Z������@�i3��5���`4��4���j
�@ �@�@�@�@�@
�@�@�@�@�@
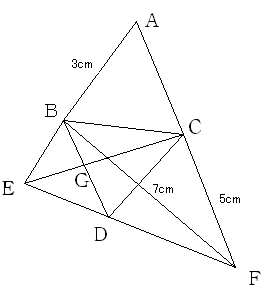
�P�ӂ�3cm�����O�p�`ABC�����O�p�`BCD������܂��B��AB����ѕ�AC�̉�������ɓ_E,F���Ƃ����Ƃ���A3�_E,D,F��
���꒼����ɕ��сACF=5cm�ABF=7cm�ƂȂ�܂����B
���̂Ƃ��ABD��CE�̌�_���f�Ƃ����Ƃ��ACG�̒��������߂Ă��������B
��1�@�ق�
�O�p�`BGC�ƎO�p�`ABF�͑����ƂȂ�܂��B
�@�܂��@�pGBC=�pBAF=60�x
�@���Ɂ@BG:BC=BG:AC=BD:AF(BD��AF�����s�ł�����j=AB:AF
�@����ĂQ�ӂ̔�Ƃ��̕ӂ����ފp���������̂ő����ƂȂ�܂��B
���̂��Ƃ���AF:BF=BC:GC����@8:7=3:CG�@CG=21/8
���Q�@�J�̖��@����
��������EB�̒������o���āA�p�̓��̐�������o���܂����B
���R�@�����@����
�����ʂ���W��u���Ă��܂����B
B(0,0), C(3,0) �Ƃ����ƂȂ�₩���� G(9/16,-9��3/16)
���S�@�������@�[�@����
�܂��ABD=3,AF=8���A���s���ɂ�鑊�����g���āABE=3�~3/5��9/5�B
����ƁABE:EC=3:5=BC:CF�Ȃ̂ŁA��BCE�䁢CBF�B
�����CE=3�~7/5=21/5�ł��邱�Ƃ��킩��B
���x�́�CEF�ŕ��s���̑������g���A
CG=21/5�~5/8=21/8�ƂȂ�B
��5�@�L����������
A�d�̉����Ƃe��ʂ�a�b�ɕ��s�Ȓ����̌�_���g�Ƃ���B
���`�g�e�͐��O�p�`�ɂȂ�A�a�g��5�A�g�e��8
�`�d�Ƃb�c�͕��s�ŁA���e�b�c�Ɓ��e�`�d�͑���������A
�`�d���b�c*8/5��24/5�@�@�@�@�a�d��9/5
�`�d�Ƃb�c�͕��s�ŁA���f�a�d�Ɓ��f�c�b�͑���������A
�f�d�F�f�b���a�d�F�c�b����9/5�F3��3�F5�@�@�@�@�b�f��5/8*�b�d
���a�g�e�Ɓ��b�`�d�͑����B�i��p60�x�ƁA��ӂ̔䂪5�F8�j
�`�d�F�d�b���g�e�F�e�a�@�@�@�@24/5�F�d�b��8�F7�@�@�@�@�d�b��21/5
�b�f��5/8*21/5��21/8
��6�@taku�����@�@QPer����
�]���藝�Ƒ����ʼn����܂����B
��CDF�ŗ]���藝����@DF=19^1/2
��AEF�䁢CDF�ő�����8�F5���
EF=(8*19^1/2)/5
cos��CEF=(7*19^1/2)/38��聢CEF�ŗ]���藝����
CE=21/5
��BGE�䁢DGC�ő�����3�F5����@�@�@CG=21/8
��7�@�������b�g��b ����
��ӂ̏�������O�p�`BED�ƎO�p�`CDF�ɂ�����BD//CF��蕽�s���̓��ʊp����
��BDE=��CFD,�܂���EBD=��DCF=60���ł��邱�Ƃ���
�O�p�`BED�ƎO�p�`CDF�͑�����
�������5:3�ł���B�Ή�����ӂ̒�������BE=3�~3/5=9/5�Ƌ��܂�B
���ɎO�p�`BEG�ƎO�p�`DCG�ɒ��ڂ��Ă݂��
BE//CD���� �O�p�`BEG�ƎO�p�`DCG��
��͂葊���ő������3:5�ł���B�����EG:GC=3:5�ƂȂ�B
���ɎO�p�`BEC�ɒ��ڂ����BE= 9/5, BC=3,��EBC=120���ł��邩��Z��
�ł͋ւ���̗]���藝�ɂ��
EC^2=EB^2+BC^2-2EB�~BCcos120�����ɐ��l��������EC^2=
(9/5)^2+3^2+ 27/5=441/25
����� EC=21/5EG:GC= 3:5 ���GC=5/8EC=5/8�~21/5=21/8
�����@21/8 cm
��8�@Fujisaki �@����
���a�d�c�䁢�b�c�e�ŁA�a�d�F�b�c���R�F�T�@������A�a�d�F�a�b���R�F�T
���a�d�b�Ɓ��a�b�e�́A�P�Q�O�x���͂��ނQ�ӂ̔䂪�R�F�T�œ������̂ő���
�@������A�d�b�F�a�e���R�F�T�@�@���d�b���Q�P/�T
�܂��A���a�d�f�䁢�c�b�f�ő�����͂R�F�T�Ȃ̂ŁA
�b�f���d�b�~�i�T/�W�j���i�Q�P/�T�j�~�i�T/�W�j���Q�P/�W�@���b�f���Q�P/�W
��9�@maruhagedon ����
���d�a�b�Ɓ��a�b�e�������ŁA�R�ӂ̒����̔�͂R�F�T�F�V�B
�܂��A���a�d�f�Ɓ��b�c�f�������ŁA������͂R�F�T�Ȃ̂łd�f�F�f�b���R�F�T�B
��10�@�˂���� ����
�O�p�`�a�d�c�ƎO�p�`�b�c�e�ɂ�����
�@�@�@�@�@�ڂc�b�e���P�W�O�[�P�Q�O���U�O��
���l�ɂ��āڂd�a�c���U�O���̂Ɂڂc�b�e���ڂd�a�c���U�O���E�E�E�@
�܂��ڂa�d�c�{�ڂa�c�d���P�W�O�[�U�O���P�Q�O�B
�@�@�ڂa�d�c�{�ڂb�e�c���R�U�O�[�P�Q�O�~�Q���P�Q�O
�̂Ɂڂa�b�d���ڂb�e�c�E�E�E�E�A
�@�A�A���O�p�`�a�d�c��O�p�`�b�c�e
�̂ɂa�d�F�R���R�F�T���a�d���X�^�T
�܂��O�p�`�a�d�b�ƎO�p�`�b�a�e�ɂ����āڂd�a�b���a�b�e���P�Q�O���E�E�B
�܂��a�d�F�b�a���X�^�T�F�R���R�F�T
�@�@�a�b�F�b�e���R�F�T�E�E�E�C
�B�A�C���O�p�`�a�d�b��O�p�`�b�a�e
�̂ɂd�b�F�V���R�F�T�@�d�b���Q�P�^�T
�܂��ڂa�c�b���ڂc�b�e���U�O�����c�a//�`�e
�̂ɂd�b�F�f�b���W�F�T
�̂ɂQ�P/�T�F�f�b���W�F�T
�̂ɂf�b���Q�P/�W
��11�@ISAMU ����
��BED�Ɓ�CDF�͑������BE=1.8
CB�̉�������E��ʂ���CB�ɐ����Ȑ��Ƃ̌�_��H�Ƃ����
��BHE��BH:HE:BE=1:��3:2�̒��p�O�p�`�ɂȂ�ABH=0.9�AHE=0.9��3�ɂȂ�B
���ACH=CB+BH=3.9���A��CHE�ɂ����ĎO�����̒藝��K�p����ƁA
CE=4.2
����AF���sBD(��AFD=��BDE)���A��AEC�Ɓ�BEG��8:3�ő����ƂȂ�A
CG=4.2�~(1-3/8)=2.625