第3回　算数問題　（2月10日〜3月9日）

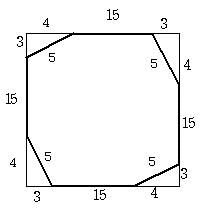
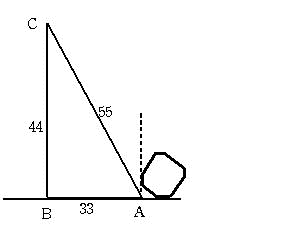
　　　　　　　　　図１　　　　　　　　　　　AB=33cm　BC=44cm　CA=55cm　図２

　図１のように、一辺が22cmの正方形の４すみから、各辺が3cm　4cm　5cmの直角三角形を切り落とします。
　次に図２のように、図１の八角形を回転させて、5cmの部分が2つの直線（直線ABとAを通りABに垂直な直線）に接するように、
三角形ABCの右に置きます。
　このとき、三角形ABCを秒速1cmで右に動かすとき、２つの図形の重なった部分が図１の図形の半分の面積になるのは何秒後
でしょうか。　（注　破線はABに垂直です）

答えが整数または既約分数で○/○で答えてください。２つ以上の解答があるときは、半角カンマ,で区切ってください。
図１の図形と図２の右の図形は同じ大きさです。

解答
　下の図のように、回転した図形は一辺が26cmの正方形から、4つの直角三角形を切り取った図形になります。この図形は
正方形の中心に関して点対称なので、中心を通る直線によってのみ面積が二等分されますから、三角形ABCを右に動かすとき、
AC,BCが正方形の中心を通るときを求めると良い事になります。
ACが中心を通るとき　x:13=3:4より　x=39/4　39/4+13=91/4
BCが中心を通るとき　33+13=46
　
答え91/4秒　46秒

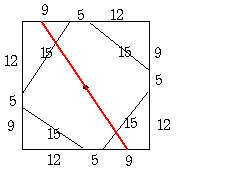
解２　(モルモット大臣　さんの考えを元に）
図のように直線の方程式をy=-4/3X+bとおく。直線y=4/3X+14との交点が(3/8b-21/4,b/2+7)
直線y=4/3X-68/3との交点(3/8b+17/2, b/2-34/3)から重なりの部分が230cm2であるように方程式を作る。
これを解いてb=5005/165=91/3となり、x軸との交点が3/4bより91/4と求まる。　（46の方は省略します）

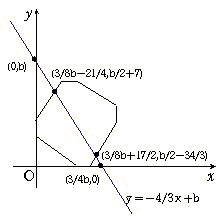
解３　（有無相生 さんの考えを元に）
上と同様にｘ軸、ｙ軸を書き込むと（13,13）を通る直線y-13=-4/3(x-13)が、2等分する直線になる。
ｙ軸に平行で（13,13）を通る直線のｘ切片13、直線y-13=-4/3(x-13)のｘ切片91/4から答えを得る。