Langleyの問題

タイプ8-1

b=90-3/2a　かつ　c=60-1/2a　かつ　　d=3/2a　（a<30）


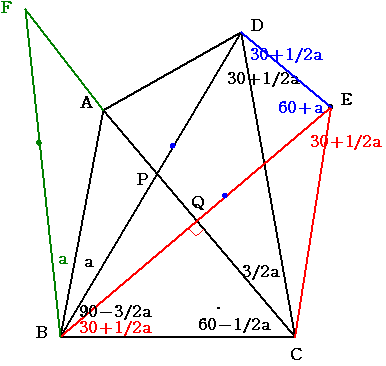
　a=20のとき
　a=20　b=60　c=50　d=30　f=30　g=80　　167番の証明























ACに関するBの対称点Eをとり、BEとACの交点をQとすると BEとACの交点をQとする.

∠BEC=∠EBC=90-c=30+a/2 また、e=180-(b+c+d)=180-(150-a/2)=30+a/2
よって、4点B、C、D、Eは同一円周上にある

∴∠DEB=∠DCB=c+d=60+a
∠EDC=∠EBC=90-c=30+a/2、e=∠BEC=30+a/2
よって、△BDEはBD=BEの二等辺三角形でである

さて直線CA上に∠ABF=a なる点Fを、Pとは別にとると
∠DBE=b-(90-c)=90-3a/2-90+60-a/2=60-2a
よって　∠QBF=60　であるから　BF=2BQ＝BE=BDとなり
　△ABD≡△ABF

ここで　∠BFQ=30であるから　f=30

特に　10刻みの整角になるのは　a=20のとき
(a、b、c、d、f)=(20、60、50、30、30)となる

タイプ8-2 　　tomhさんの証明

b=90-3/2a　かつ　c=60-1/2a　かつ　　d=3/2a　（30<a<60）

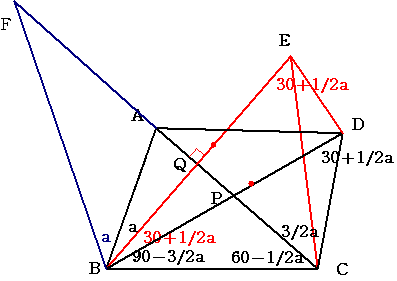
　(a, b, c, d; f) = (40, 30, 40, 60; 30) … No.265

















ACに関するBの対称点Eをとり、BEとACの交点をQとする。
BEとACの交点をQとする。

∠BEC=∠EBC=90-c=30+(1/2)a (∵ △CBEは二等辺三角形)
また、∠BDC=180-(b+c+d)=180-(150-(1/2)a)=30+(1/2)a.
よって、4点B, C, D, Eは同一円周上にある。

　∠EDB = ∠ECB = 180-2∠EBC = 120-a,
　∠BEC = 30+(1/2)a,
　∠CED = ∠CBD = 90-(3/2)a,
　∠BED = ∠BEC+∠CED = 30+(1/2)a +90-(3/2)a = 120-a.

よって、△BDEはBD=BEの二等辺三角形である。

　∠DBE = 180-2∠BDE = 180-240+2a = 2a-60.

直線CA上に∠ABF=a なる点Fを、Pとは別にとると
　∠QBF = ∠ABF+∠ABD-∠DBE = 2a+(90-3/2a)-(30+1/2a)=60,
　∠BQF = 90
であるから、BF=2BQ＝BE=BDとなり、

　△ABD≡△ABF. (∵ 二辺挟角)

ここで、∠BFQ=30であるから　f=30


特に10刻みの整角になるのは、a=40のときで、
　(a, b, c, d; f) = (40, 30, 40, 60; 30) … No.265