タイプ7
a=15+t かつ b=45+3t かつ c=60-2t d=30 (t<30)
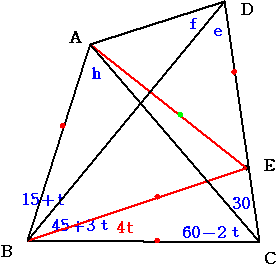
t=5のとき
a=20 b=60 c=50 d=30 f=30 g=80 167番の証明
t=15のとき
a=30 b=90 c=30 d=30 f=30 g=90 a=dタイプ1なので表にはない
t=25のとき
a=40 b=120 c=10 d=30 f=30 g=100 左右対称にして195番の証明
辺CD上に角EBC=4t 度 となる点Eをとります。
角CEB=180-(60-2t)-30-4t=90-2tとなるので
三角形BCEは 4t 度 (90-2t) 度 (90-2t) 度 の二等辺三角形 となるので BC=BE ①
角DBE=(45+3t)-4t=45-t 角BDE(eのこと)=角BEC-角DBE=(90-2t)-(45-t)=45-tとなるので
三角形BDEは (45-t) 度 (45-t)度 の二等辺三角形 となるので BE=DE ②
角BAC(hのこと)=180-(15+t)-(45+3t)-(60-2t)=60-2tとなるので
三角形ABCは 二等辺三角形 となるので BC=BA ③
角ABE=(15+t)+(45+3t)-4t=60 および
①③より 三角形ABEは正三角形となり BE=EA ④
②④より点E,点A,点DはEを中心とする半径BEの円上にあるから
角ADB(fのこと)=1/2×角AEB=30° 中心角 と 円周角の性質から
よってf=30°となります。