僞僀僾6
a=c=30丂偐偮丂d=2b-30丂乮15<b<45乯
 嵍塃懳徧偵偡傞偲丂No52
嵍塃懳徧偵偡傞偲丂No52a=10丂b=30丂c=20丂d=30偺偲偒丂倖亖10
No219
a=30丂倐=40丂c=30丂d=50丂偺偲偒丂倖亖20丂
丂
Langley偺栤戣
僞僀僾6
a=c=30丂偐偮丂d=2b-30丂乮15<b<45乯
 嵍塃懳徧偵偡傞偲丂No52
嵍塃懳徧偵偡傞偲丂No52
a=10丂b=30丂c=20丂d=30偺偲偒丂倖亖10
No219
a=30丂倐=40丂c=30丂d=50丂偺偲偒丂倖亖20丂
丂
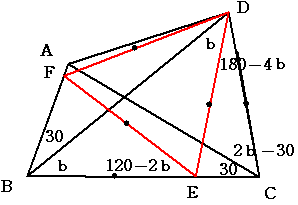
曈BC忋偵妏CDE=180-4倐丂搙丂偲側傞揰E傪偲傞丅曈AB忋乮傑偨偼AB偺墑挿慄忋乯偵
妏BEF=120-2b丂搙丂偲側傞揰F傪偲傝傑偡丅
嶰妏宍CDE偼丂2b丂搙丂(180-4b)丂搙丂2b丂搙丂偺擇摍曈嶰妏宍丂偲側傞偺偱丂DC=DE丂丂嘆
嶰妏宍BDE偼丂b搙丂b搙丂(180-2b)搙偺擇摍曈嶰妏宍丂偲側傞偺偱丂BE=DE丂丂丂嘇
嶰妏宍BEF偼丂(倐+30)丂搙丂(120-2倐)丂搙丂(b+30)搙偺擇摍曈嶰妏宍丂偲側傞偺偱丂BE=EF丂丂丂嘊
嘇嘊傛傝丂DE=EF丂傑偨丂妏DEF=60搙傛傝丂嶰妏宍DEF偼惓嶰妏宍
傛偭偰DE=DF
偙傟偲嘆偐傜DC=DF
偡傞偲嶰妏宍CDF偼擇摍曈嶰妏宍偱偁傝丂妏DCF=(180-(240-4b))/2=俀倐-30丂搙偲側傞
偲偄偆偙偲偼丂F偼幚偼A偲堦抳偟偰偄傞偙偲偑傢偐傞
傛偭偰丂妏ADB=妏FDB=60-b丂搙丂偲側傝傑偡
僞僀僾6-2丂丂丂tomh偝傫偺徹柧
a=c=30丂偐偮丂d=2b-30丂乮45<b<60乯
No230偺暿夝
(a, b, c, d; f) = (30, 50, 30, 70; 10)
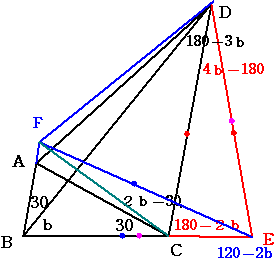
捈慄BC忋偵佢CDE=4b-180偲側傞揰傪(曈BC奜偵)偲傝傑偡丅
傑偨丂捈慄AB忋偵佢BEF=120-2b偲側傞揰F傪偲傝傑偡丅
仮CDE偼丄180-2b, 4b-180, 180-2b 偺擇摍曈嶰妏宍偲側傞偺偱丄
DC=DE.丂乧 (1)
仮BED偼丄b, b, 180-2b 偺擇摍曈嶰妏宍偲側傞偺偱丄
BE=DE.丂乧 (2)
仮BEF偼丄b+30, 120-2b, b+30 偺擇摍曈嶰妏宍偲側傞偺偱丄
BE=EF.丂乧 (3)
(2)(3)傛傝丄DE=EF. 傑偨丄佢DEF=60 傛傝丄仮DEF偼惓嶰妏宍丅
傛偭偰丄DE=DF.
偙傟偲(1)偐傜丄DC=DF.
偡傞偲丄仮CDF偼擇摍曈嶰妏宍偱偁傝丄
佢DCF=[180-(60-(4b-180))]/2=2b-30 偲側傞丅
偲偄偆偙偲偼丄F偼幚偼A偲堦抳偟偰偄傞偙偲偑傢偐傞丅
傛偭偰丄佢ADB=佢FDB=60-b 偲側傝傑偡丅
摿偵10崗傒偺惍妏偵側傞偺偼丄b=50偺偲偒偱丄
丂(a, b, c, d; f) = (30, 50, 30, 70; 10) 乧 No.230
偱偡丅