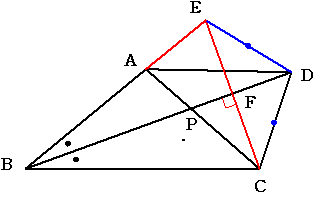
Langleyの問題

タイプ5

a=b　かつ　c+2d=180°

　　その１　　　　c<90のとき　　　　　　　　　　　　　　　　

その２　　　　　　　　　c>90のとき

ｃからBDへ垂線を下ろしその足をFとします。CFの延長線が直線ABと交わる点をEとします。

三角形BCEは二等辺三角形になっており　よって　三角形CDEも二等辺三角形となっています。
角CDE=2×角BDC=2(180-(b+c+d))=2(180-a-(180-2d)-d)=2(d-a)

その１　B,A,Eの順に並んでいる時(ｃが90より小さいとき）

角BAC=180-(a+b+c)=180-a-a-(180-2d)=2(d-a)
角CDE=角BACとなるので　四角形ACDEは円に内接しています。
よって角ADB=角EDB-角EDA=(d-a)-角ECA=(d-a)-(90-a-c)
=c+d-90=180-2ｄ+ｄ-90=90-ｄとなります

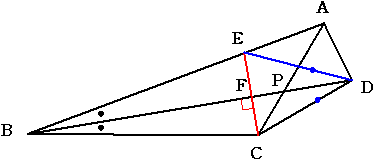
その２　B,E,Aの順に並んでいる時(ｃが90より大きいとき）

角EAC=180-(a+b+c)=180-a-a-(180-2d)=2(d-a)
角CDE=角EACとなるので四角形ACDEは円に内接しています。
よって角ADB=角EDB+角EDA==(d-a)+角ECA=(d-a)+(c-(90-a))
= =c+d-90=180-2ｄ+ｄ-90=90-ｄとなります


別解　（リンデンさんの解答）
a=b　かつ　c+2d=180°のとき　f=1/2c

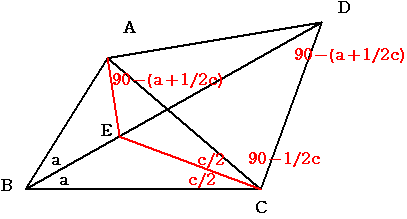
三角形ABCの内心をEとします。角CAE=90-(a+1/2c)となっています。
また　三角形BCDにおいて　角BDC=180-(a+c+90-1/2c)=90-(a+1/2c)
よって角EAC=角EDCとなります

このことから　四角形AECDは円に内接していることがわかりますから
角ADE=角ACE　すなわち　f=1/2cであることがわかります