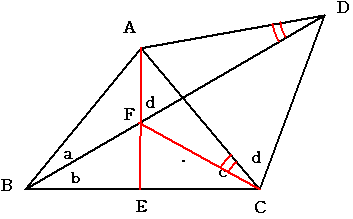
Langleyの問題

タイプ４

a+b=c　かつ　ｂ+d=90°

三角形ABCは二等辺三角形ですから　AからBCに垂線を下ろし　足をEとします
AEとBDの交点をFとします。

三角形ABEと三角形ACEは合同ですからBE=CEとなります。
よって三角形FBEと三角形FCEは合同となり　角FCE=角FBE=ｂとなります
よって　角ACF=ｃ−ｂ=aとなります。（a+b=cから）

次に四角形AFCDにおいて　角AFD=角BFE=90-b=d=角ACDとなり　この四角形は円に内接していることがわかります。
よって角ADF=角ACF=aとなります。