Langley偺栤戣
僞僀僾21
倓亅倎亖倕 偲 惓嶰妏宍俢俷仩偵傛傞徹柧
嚈俛俠俢偺奜愙墌偺拞怱傪俷丆墌偲捈慄俛俙偺岎揰傪俥丆 墌偲捈慄俠俙偺岎揰傪俧偲偟傑偡丅
曗戣侾丂倓亅倎亖倕偺偲偒佢俙俷俛亖們乮們亙俋侽乯 傑偨偼 佢俙俷俛亖侾俉侽亅們乮們亜俋侽乯
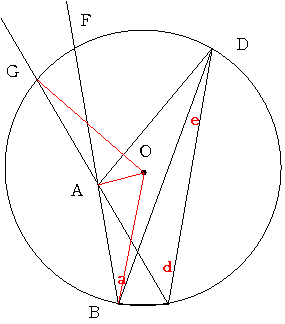
徹柧
屖GF偵懳偡傞墌廃妏=屖GD偵懳偡傞墌廃妏-屖FD偵懳偡傞墌廃妏
丂丂丂丂丂丂丂丂丂丂丂丂丂=丂d-a丂=丂e乮壖掕傛傝乯
丂丂丂丂丂丂丂丂丂丂丂丂丂=屖BC偵懳偡傞墌廃妏
傛傝丂屖GF=屖BC
偙偺偙偲偐傜丂屖GC偺挿偄傎偆=屖GF+屖FC
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂=屖BC+屖FC
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂=屖BF偺挿偄傎偆
偦偺拞怱妏傪峫偊傞偲丂佢FOB=佢GOC
傛偭偰丂嚈俛俷俥佭嚈俠俷俧
嶰妏宍AFG偲嶰妏宍ACB偵偍偄偰
丂FG=CB丂(忋偵婰偟偨屖GF=屖BC傛傝乯
丂佢GFA=佢BCA丂(墌廃妏乯
丂佢FGA=佢CBA乮墌廃妏乯
傛傝丂仮AFG佭仮ACB
傛偭偰丂AG=AB
嶰妏宍OAG偲嶰妏宍OAB偵偮偮偄偰
AG=AB丂OA嫟捠丂OG=OB傛傝
嶰妏宍OAG佭嶰妏宍OAB
傛偭偰丂佢AOG=佢AOB
偲偙傠偱丂佢GOB偼屖GB偵懳偡傞墌廃妏偱偁傞偐傜丂2c丂傑偨偼360-2c
傛偭偰佢AOB=c丂傑偨偼丂180-c偲側傞
僞僀僾21-1
a=30丄們=270-3b丂d=倐-30丂偺偲偒丂丂f=90-b 丂
e=180-b-c-d=倐-60=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
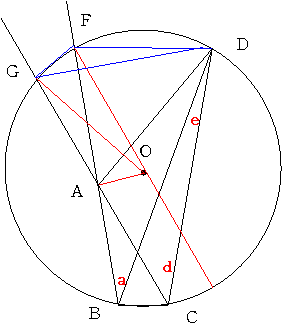
b=70偲偟偰
240丂 a=30 b=70 c=60 d=40 f=20
倐亖80偲偟偰丂
241丂 a=30 b=80 c=30 d=50 f=10
偺俀偮偑弌傑偡
佢FOG=屖FG偵懳偡傞拞怱妏=屖BC偵懳偡傞拞怱妏丂乮忋偺曗戣偐傜丂屖GF=屖BC)
丂丂丂丂=2e=2b-120
佢OGA=佢OGB乕佢CGB
丂丂丂丂=(180-佢GOB)/2-e丂丂丂丂丂(嶰妏宍OGB偼擇摍曈嶰妏宍乯
丂丂丂丂=(180-2c)/2-e
丂丂丂丂=2b-120
傛偭偰丂OF//AG
嶰妏宍AGF偲嶰妏宍GAO偵偮偄偰
佢GAF=佢BAC=180-a-b-c=180-30-b-(270-3b)=2b-120=佢AGO
AG嫟捠
佢AGF=180-佢GAF-佢GFA=180-(2倐-120)-c丂佢GAO=180-佢OGA-佢GOA=180-(2倐-120)-c
傛偭偰仮AGF佭仮GAO
GF=AO
仮AOD偲仮GFD偵偮偄偰
AO=GF丂乮忋偺偙偲偐傜乯
丂佢GFD=180-佢GCD=210-b
丂佢AOD=佢AOG+佢FOD+佢FOD=c+2d=21-b
傛偭偰丂佢GFD=佢AOD
OD=FD丂乮嶰妏宍OFD偼惓嶰妏宍乯
傛偭偰丂仮AOD佭仮GFD
AD=GD
嶰妏宍GDA偼擇摍曈嶰妏宍偲側傞偐傜丂佢GDA=180-2亊佢DGA=180-2b
佢ADB=佢GDB-佢GDA=c-(180-2b)=90-b
僞僀僾21-2
a=30丄們=3b-270丂d=240-2倐丂偺偲偒丂丂f=倐-90 丂
e=180-b-c-d=210-2倐=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
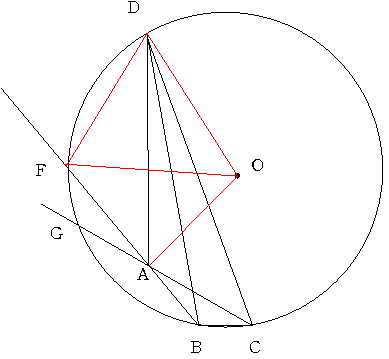
b=100偲偟偰
244丂 a=30 b=100 c=30 d=40 f=10
偑偱傑偡
曗戣傛傝丂佢GOA=c=3倐-270
曗戣偺徹柧偺拞偐傜丂佢FOG=2e=2(180-b-c-d)=420-4b
傛偭偰佢FOA=150-b丂...嘆
巐妏宍DFBC偼墌偵撪愙偟偰偄傞偺偱丂佢DFA=180-c-d=210-b
嶰妏宍OFD偼惓嶰妏宍側偺偱佢DFO=60
傛偭偰彂偔OFA=210-b-60=150-b丂丂...嘇
嘆嘇傛傝丂嶰妏宍OFA偼擇摍曈嶰妏宍
傛偭偰丂OA=FA丂丂...嘊
嶰妏宍DFA偲嶰妏宍DOA偵偮偄偰
DF=DO丂(嶰妏宍DOF偼惓嶰妏宍乯
嘊偐傜丂FA=OA
DA偼嫟捠
傛偭偰嶰妏宍DFA佭嶰妏宍DOA
佢ADO=60/2=30偱偁傞
巐妏宍DBCO偵偮偄偰丂佢DOC偺戝偒偄傎偆=2b
佢DOC偺彫偝偄傎偆=360-2b
嶰妏宍ODC偼擇摍曈嶰妏宍偱偁傞偐傜佢ODC=(180-(360-2b))/2=倐-90
佢BDC=e=210-2b
傛偭偰佢ADB=30-(b-90)-(210-2b)=b-90
僞僀僾21-3
a=30丄們=b+90丂d=60-倐丂偺偲偒丂丂f=90-倐 丂
e=180-b-c-d=210-2倐=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
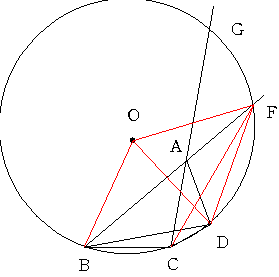
b=10偲偟偰
191丂 a=30 b=10 c=100 d=50 f=80
b=20偲偟偰
209丂 a=30 b=20 c=110 d=40 f=70
偑偱傑偡
嶰妏宍OFD偼惓嶰妏宍
佢BCD=c+d=150丂傛傝丂佢BOD偺戝偒偄傎偆=300
佢BOC偺彫偝偄傎偆=60
傛偭偰嶰妏宍OBD偼惓嶰妏宍
A偼OD偺悅捈擇摍暘慄忋偵偁傞偐傜嶰妏宍AOB佭嶰妏宍ADB
佢ADB=佢AOB=180-c丂乮曗戣傛傝乯=90-b
僞僀僾21-4
b=2a-180丄們=a-60丂d=210-a丂偺偲偒丂丂f=30 丂
e=180-b-c-d=210-2a=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
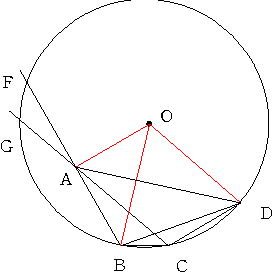
a=100丂偲偟偰丂
350丂 a=1000 b=20 c=40 d=110 f=30
偑偱傑偡
妏BCD=c+d=150傛傝丂妏BOD偺戝偒偄傎偆=300
傛偭偰嶰妏宍OBD偼惓嶰妏宍
曗戣傛傝妏AOB=c=a-60
妏ABO=a-60
傛偭偰嶰妏宍OAB偼擇摍曈嶰妏宍偱丂OA=BA
嶰妏宍OAB佭嶰妏宍BAD偲側傞偐傜丂妏ODA=妏BDA=30搙
傛偭偰倖亖30偲側傞
僞僀僾21-5
b=2a丄們=a+120丂d=30-a丂偺偲偒丂丂f=30 丂
e=180-b-c-d=30-2a=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
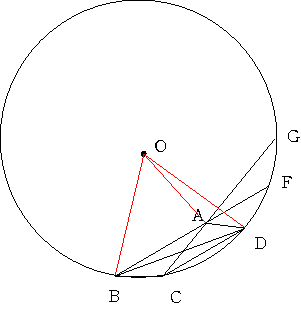
a=10丂偲偟偰丂
51斣丂a=10丂b=20丂c=130丂d=20
妏BCD=b+c=150傛傝丂妏BOD偺戝偒偄傎偆=300
傛偭偰嶰妏宍OBD偼惓嶰妏宍
曗戣傛傝丂妏AOB=180-c=60-a
妏OBA=妏OBD-a=60-a
傛偭偰丂嶰妏宍OAB偼擇摍曈嶰妏宍
嶰妏宍OAD佭嶰妏宍BAD偲側傝丂妏ADB=30搙丂偲側傞
僞僀僾21-6
b=a/2丄們=120-a/2丂d=30+a/2丂偺偲偒丂丂f=90-a/2
e=180-b-c-d=30-a/2=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
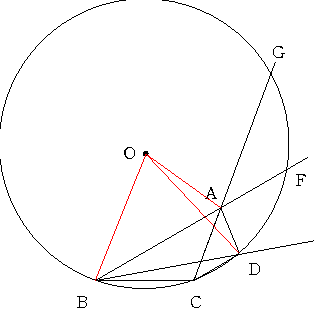
a=20 偲偟偰
112斣丂a=20 b=10 c=110 d=40 f=80
a=40 偲偟偰
256斣丂a=40 b=20 c=100 d=50 f=70
妏BCD=c+d=150傛傝丂妏BOD偺戝偒偄傎偆=300丂傛偭偰嶰妏宍OBD偼惓嶰妏宍
妏OBC+妏BCA=60+b+c=180傛傝丂OB//CA
曗戣傛傝丂妏AOB=180-c=60+a/2
妏OBC=60+b=60+a/2
傛偭偰丂巐妏宍OBCA偼摍媟戜宍丂
傛偭偰丂OA=CB
嶰妏宍OAD偲嶰妏宍BCD偼
丂OD=BD丂妏AOD=妏DBC=a/2丂OA=BC
傛傝丂崌摨偲側傝丂妏ADO=妏BDC=e=30-a/2
傛偭偰f=e+60=a/2+60
僞僀僾21-7
b=2a丄們=120-a丂d=30丂偺偲偒丂丂f=30
e=180-b-c-d=30-a=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
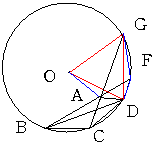
a=10 偲偟偰
48斣丂a=10 b=20 c=110 d=30 f=30
a=20 偲偟偰
159斣丂a=20 b=40 c=100 d=30 f=30
d=30傛傝丂妏GOD亖60
嶰妏宍ODG偼惓嶰妏宍
妏OGA=妏OGD-妏CGD=60-2a
妏BAC=180-a-b-c=60-2a
傛偭偰俙俥//俷俧
嶰妏宍OAD丂嶰妏宍GFD
妏AOD=妏AOG-60=180-c-60=120-c=a丂(曗戣傛傝乯
妏FGD=a丂傛傝丂妏AOD=妏FGD
偙傟偐傜丂妏AOG=妏FGO=60+a
巐妏宍OAFG偼摍媟戜宍
傛偭偰丂OA=FG
嶰妏宍OAD丂嶰妏宍GFD
偵偮偄偰丂OA=GF
妏AOD=妏FGD=a
OD=GD
傛傝嶰妏宍OAD佭嶰妏宍GFD
f=妏BDG-妏ODG-妏ODA=c-60-妏GFD=c-60-e丂乮曗戣傛傝丂BC=GF乯
=120-a-60-(30-a)=30
僞僀僾21-8
b=a/2丂們=120+a/2丂d=30丂偺偲偒丂丂f=30
e=180-b-c-d=30-a=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
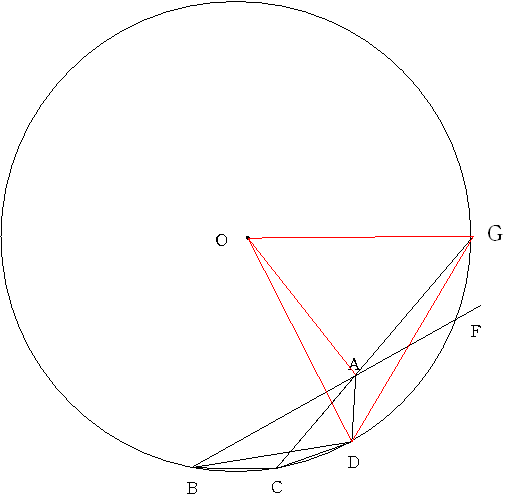
a=20 偲偟偰
115斣丂a=20 b=10 c=130 d=30 f=100
妏d=30搙傛傝妏GOD亖60
嶰妏宍ODG偼惓嶰妏宍
AOG=180-c=+60-a/2丂乮曗戣傛傝乯
妏AGD=60-b=60-a/2
傛偭偰嶰妏宍OAG偼擇摍曈嶰妏宍
妏AOD=妏DOA-妏AOG
妏AGD=妏DGO-妏AGO傛傝丂妏AOD=妏AGD
AO=AG丂丂丂丂丂DO=DG
傛偭偰嶰妏宍OAD佭嶰妏宍GAD
妏ADO=妏ADG=30搙
f=妏ADB-妏ADO=c-30=90+a/2
僞僀僾21-9
b=a/2+90丂們=30+a/2丂d=30丂偺偲偒丂丂f=a/2
e=180-b-c-d=30-a=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
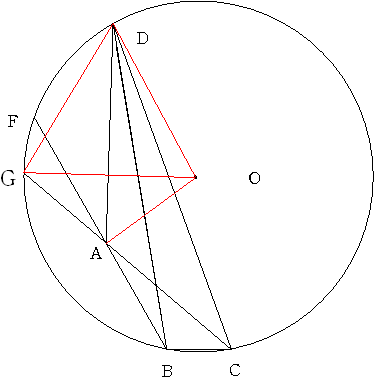
a=20 偲偟偰
177斣丂a=20 b=100 c=40 d=30 f=10
d=30傛傝丂妏GOD亖60
嶰妏宍ODG偼惓嶰妏宍
妏AOG=c=30+a/2
妏AGO=妏AGD-妏OGD=倐亅60=a/2+30
傛偭偰丂妏AOG=妏AGO
嶰妏宍AOG偼擇摍曈嶰妏宍
AD偼OG偺悅捈擇摍暘慄偵側傝妏ADO=30搙
堦曽丂嶰妏宍OBD偵偍偄偰
妏DOB=2(c+d)=120+a
妏BDO=(180-妏DOB)/2=30-a/2
f=妏ADO-妏BDO=a/2
僞僀僾21-10
b=30丂們=90+a丂d=30丂偺偲偒丂丂f=2a
e=180-b-c-d=30-a=d-a傛傝丂僞僀僾21偺忦審傪傒偨偡
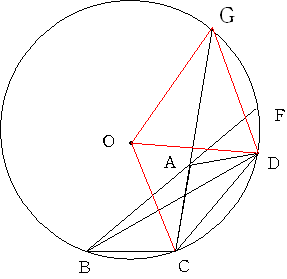 a=10偲偟偰
a=10偲偟偰
66斣丂a=20 b=30 c=100 d=30 f=20
a=20 偲偟偰
149斣丂a=20 b=30 c=110 d=30 f=40
妏GOD=2d=60傛傝嶰妏宍俢俷俧偼惓嶰妏宍
妏DOC=2倐=60傛傝嶰妏宍DOC偼惓嶰妏宍
柧傜偐偵丂嚈俙俷俠佭嚈俙俢俠
AOG=180-c乮曗戣乯傛傝丂妏AOD=180-c-60=30-a
AG偼OD偺悅捈2摍暘慄偱偁傞偐傜丂妏ADO=30-a
f=妏GDB-妏GDO-妏ODA=c-60-(30-a)=2a
***********************埲壓枹惍棟
仠惓嶰妏宍俢俷俠丄偺偲偒乮倐亖俁侽乯丗
亂噦俁俁俆丄倖亖係侽丟噦俁係俆丄倖亖俀侽丟乮們亄俁倕亖俋侽乯丟佀俙俛//俷俠丆嚈俙俷俢佭嚈俛俠俢丆倖亖俇侽亅俀倕亃丟
亂噦俁俆俀丄倖亖俀侽丟乮俀倎亅倓亅們亖俇侽乯丟佀嚈俙俷俢佭嚈俙俠俢丆倖亖俁侽亅倕亃丟
亂噦俇俋丄倖亖俀侽丟乮倎亄倓亖俁侽乯丟佀嚈俙俷俢佭嚈俙俠俢丆倖亖俁侽亅倕亃丟










 a=10偲偟偰
a=10偲偟偰