タイプ20
b=a/3 c=90-2/3a、d=60+1/3aのとき f=60-1/3a
証明
番号
186 a=30 b=10 c=70 d=70 f=50
315 a=60 b=20 c=50 d=80 f=40
2通りの三角形が解決します。
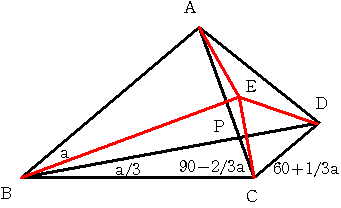
BDに関する点Cの対称点をEとします。
角BCD=30度であるから 角EDC=60度になり Eのとり方から DE=DC
よって三角形CDEは正三角形となります。
次に三角形ABCは 角BAC=角BCA=90-2/3a の二等辺三角形であるので BC=BA
また Eのとり方から 角CBE=2/3a よって 角EBA=2/3a
よって三角形ABEと三角形CBEは合同となり AE=CE
Eは三角形ACDの外心となり 角CAD=30度
角PAD+角PDA=角PBC+角PCBから 角PDA=60-1/3a