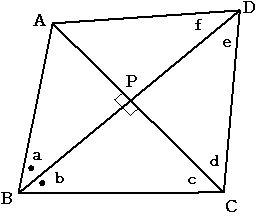
Langleyの問題

タイプ２
a=b　かつb+c=９０°　または　c=dかつ　b+c=90°　の形

a=b　かつ　b+c=90°　として角を求めます。

三角形ABPと三角形CBPは合同
三角形ABPと三角形CBPにおいて　角APB=角CPB、　　BP　共通、角ABP=角CBP
よって　三角形ABPと三角形CBPは合同

このことから　AP=CPとなります

三角形ADPと三角形CDPは合同
三角形ADPと三角形CDPにおいて　AP=CP,角APD=角CPD、PDは共通
よって三角形ADPと三角形CDPは合同

このことから　ｆ＝ｅ=　９０-d　となります。

c=dかつ　b+c=90°のときは
上の図を左右対称に折り返して角DAPを求めることになりますから
上の図ではdに等しくなります。　実際はaに等しいわけです。