タイプ18
a=30 c=d=120-b のとき f=b-60 (60<b<120)
証明
 番号
番号239 a=30 b=70 c=50 d=50 f=10
242 a=30 b=80 c=40 d=40 f=20
130の左右対称
a=30 b=100 c=20 d=20 f=40
→a=20 b=20 c=100 d=30 f=80
22の左右対称
a=30 b=110 c=10 d=10 f=50
→a=10 b=10 c=110 d=30 f=70
の4通りの三角形が解決します。
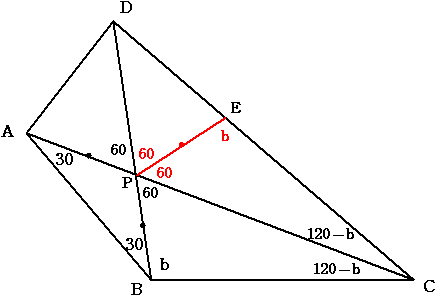
CD上に角CPE=60度となる点Eをとります。
三角形BCPと三角形ECPは合同です
(CPが共通で 角ACP=角ECP=120-b 角BPC=角EPC=60度より)
よって BP=EP ...①
三角形ABPは二等辺三角形ですから BP=AP
①より AP=EPとなります。
このとき 三角形ADPと三角形EDPは合同です
(DPが共通で 角APD=角EPD=60度 AP=EP)
よって 角ADP=角EDP=b-60となります。