Langleyの問題

タイプ17

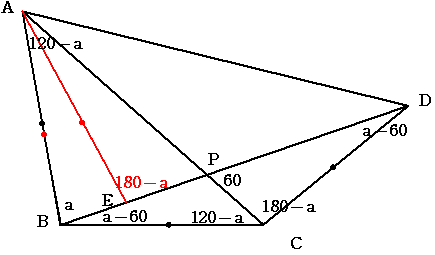
ｂ=a-60 c=120-a d=180-aのとき　　f=30 　(60<a<90)
　
証明

342番
　(a,b,c,d,f)=(80,20,40,100,30)

329番
　(a,b,c,d,f)=(70,10,50,110,30)

三角形BCDにおいて　角CBD=角CDB=a-60より　三角形BCDは二等辺三角形であり
BC=CD　…�@

三角形ABCにおいて　角BCA=角BAC=120-aより　三角形ABCは二等辺三角形であり
BC=AB　…�A

BD上にAB=AEとなる点Eをとる

三角形ABEは二等辺三角形であるから　角AED=180-a
また　角ACD=180-aであるから　四角形AECDは同一円周上にある。

�@�Aより　AE=CDであるから　角ADE=角CAD（同じ長さの弦に対する円周角は等しい）

三角形APDは二等辺三角形であり　角DPC=60度であるから　角ADP=30度