タイプ16
b=60-a/3 c=30、d=60+a/3のとき f=a/3
証明
 番号
番号230 a=30 b=50 c=30 d=70 f=10
320 a=60 b=40 c=30 d=80 f=20
351の左右対称
a=100 b=30 c=20 d=120 f=10
の3通りの三角形が解決します。
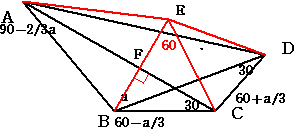
BCを一辺とする正三角形BCEを図のように描き ACとBEの交点をFとします。
このとき 三角形BCFと三角形ECFが合同ですから BF=EF
よって三角形ABFと三角形AEFが合同ですから …(*)
角AEF=角ABF=90-(90-2/3a)=2/3a …①
次にEを中心として半径EBの円を描くと 角BDC=30°より Dはこの円周上の点であることがわかります。
(弦BCに対する中心角の半分となっている)
よって角DECは弦CDに対する中心角であり 角CBDの2倍で 120-2a/3となります
このことと①から 角AEDは 2/3a+60+(120-2a/3)=180度となり EはAD上の点であることがわかります。
すると (*)から 角BAD=角BAC×2=180-4a/3であり
三角形ABDに着目すると
角ADB=180-a-(180-4a/3)=1/3aであることがわかります