タイプ15
b=a+60 c=60-a、d=30のとき f=a
証明
番号
89 a=10 b=70 c=50 d=30 f=10
173 a=20 b=80 c=40 d=30 f=20
207を左右対称にしたもの
a=30 b=20 c=100 d=40 f=80
194を左右対称にしたもの
a=30 b=10 c=110 d=50 f=70
4通りの三角形が解決します。
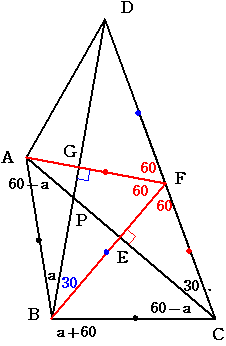
BよりACへ垂線を下ろし 足をEとし BEの延長とCDの交点をFとします
また AFとBDの交点をGとします
三角形ABCにおいて 角BAC=角BCA=60-a なので 三角形ABCは二等辺三角形
よって AE=ECとなります。
すると 三角形AEFと三角形CEFは合同となるので 角AFE=角CFE=60度 となります。
よって 角DFA=180-60×2=60度となっています。
三角形BFGにおいて 角GBF=角ABF-角ABD
=角ABC÷2-角ABD
=(a+a+60)÷2−a=30°
よって角FGB=90度となります。
このことから 三角形BGFと三角形DGFが合同でBG=DGがわかります。
すると三角形AGBと三角形AGDが合同ですから
角ADG=角ABG=a となります。