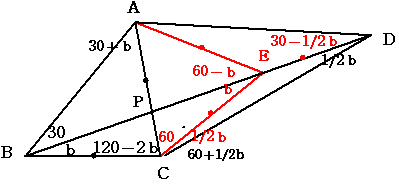
タイプ14
c=120-2b、d=60+1/2bのとき f=30-1/2b
証明
c=90-a、d=2aのとき f=90-a-b
番号
206 a=30 b=20 c=80 d=70 f=20
222 a=30 b=40 c=40 d=80 f=10
2通りの三角形が解決します。
三角形ABCにおいて 角ABC=角BAC=30+bであるから 三角形ABCは二等辺三角形
よってAC=BC …①
角ACE=60度となる点EをBD上にとる
Langleyの問題
タイプ14
c=120-2b、d=60+1/2bのとき f=30-1/2b
証明
c=90-a、d=2aのとき f=90-a-b

番号
206 a=30 b=20 c=80 d=70 f=20
222 a=30 b=40 c=40 d=80 f=10
2通りの三角形が解決します。
三角形ABCにおいて 角ABC=角BAC=30+bであるから 三角形ABCは二等辺三角形
よってAC=BC …①
角ACE=60度となる点EをBD上にとる
三角形BCEで角CBE=角CEB=bより 三角形BCEは二等辺三角形 よって BC=EC
これと①から AC=ECとなるから 三角形ACEは正三角形となる
よって EC=EA …②
三角形CDEにおいて角EDC=1/2b 角BEC=b=角EDC×2 となり三角形CDEは
二等辺三角形 よって CE=ED
これと②から AE=DE となるから 三角形AEDは二等辺三角形となる
三角形AEDにおいて 角AEB=60-bより 角ADE=30-1/2b